2801842214

MATEMATYKA 3. MACIERZE I WYZNACZNIKI

3.8 Równanie charakterystyczne macierzy

Z danej macierzy kwadratowej A stopnia n o elementach o,-* (*• k = 1.2...., n)

«n

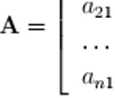
utworzymy nowa macierz zgodnie z zapisei

«12    •    •    •    aln

«22    '    '    ’    «2n

®n2    '    '    '    ®rm

A — Al = C. W rezultacie otrzymamy

(131)

C =

u — A	a. 12	“Ir,
a-) i	0.22 “A	»2n
"n 1	On2	' ^(l rm A

Przyrównując do zera wyznacznik macierzy

(132)

(132)

a n — A	012	dln
a-> i	022 — A	d2n	= 0	(133)
	«n2	(Inn ^— ^

otrzymamy równanie stopnia n względem A, które nazywamy równaniem charakterystycznym macierzy A. Pierwiastki A* tego równania, różne od zera dla macierzy nieosobliwej, nazywamy wartościami własnymi macierzy A. Równanie

det (A - Al) = 0

ma dokładnie n pierwiastków rzeczywistych lub zespolonych, jeżeli każdy pierwiastek liczy sit; tyle razy, ile wynosi jego krotność.

Znając wszystkie wartości własne macierzy możemy obliczyć wartość jej wyznacznika

n

det (A) = A, ■ A₂.....A„ = P[ A;    (135)

?=1

oraz tak zwany ślad macierzy (ang. tracę)

n

tr(A) = Ai + A2 + • • • + A„ = ^ ' A,    (136)

?=i

Wniosek 3.4 Z relacji (135) wynika, źc macierz A jest macierzą osobliwą, jeżeli, co najmniej jedna wartość własna jest równa 0.

Wniosek 3.5 Suma wartości własnych macierzy A jest równa sumie elementów znajdujących sic na przekątnej gwnej tej macierzy: Ai + A2 H----+ A„ = an + 022 + ... + dnn = tr(A).

Moduł maksymalnej wartości własnej macierzy A nazywamy jej promieniem spektralnym i oznaczamy

/>(A) = max |A|    (137)

A&t(A)

55