PC043402

III

Funkcja potęgowa w równaniach

Definicja 1.77. Równaniami potęgowymi nazywamy równania, w niewiadoma występuje w dowolnej potędze.

Klasycznym przykładem równania potęgowego z niewiadomą* jest rów nie postaci*" = b, gdzie a,b e R. Jego rozwiązanie polega na podnieaieśjB odpowiedniej potęgi obu stron równania. Wykonując operacje potęgową; należy pamiętać o dziedzinie równania, która zależy od wykładnika o. M

Przykład 1.102

Równanie potęgowe *³ = 16, którego dziedziną jest zbiór R, rozwiązał

. i iJ

podnosząc obie strony do potęgi -^.Otrzymujemy (*³)³ =16’. Wykonyst^ i-i:    i I

własności potęg, mamy *=(2⁴)³, a stąd * = 2³ = 2 • 2³ = 21/2.__^

Przykład 1.103    |

Równanie potęgowe *⁴ = 3 lub inaczej V* = 3, którego dziedzinąjjs&t żł$ liczb rzeczywistych nieujemnych, rozwiążemy, podnosząc obie jego stronjk

potęgi czwartej. Mamy zatem (*⁴) =3⁴ i dalej z własności potęg otrzynraji|j

*=81.

W niektórych przypadkach równania potęgowego możemy posłużyli podstawieniem.

Przykład 1.104

W celu rozwiązania równania V* =* -2, które ma sens dla x > 0, możeą wprowadzić pomocniczą niewiadomą t = V*, gdzie t>0. Wówczas równa! to stanie się równaniem kwadratowym / = t² - 2, które po przeksztalcenim postać t² -1 - 2 = 0. Uzyskane w ten sposób równanie kwadratoweiposiai dwa różne rozwiązania: f, = -1 oraz t₂ = 2. Pierwsze z nich jest ujemne, więc at spełnia założenia t > 0. Powracając do podstawienia, otrzymujemy zależno! v* = 2. a stąd - po podniesieniu do potęgi drugiej - mamy * = 4.

Przegląd funkcji elementarnych_

117

1.6.6. Funkcja wykładnicza

Definicja 1.78. Funkcją wykładniczą zmiennej* nazywamy dowolną funkcję postaci:

/(*) = «%    (115)

gdzie ae R' \{ 1}

Niezależnie od wartości stałej a funkcja wykładnicza:

•    jest określona dla wszystkich liczb rzeczywistych,

•    ma wartości ze zbioru liczb rzeczywistych dodatnich,

•    jest równowartościowa.

Wykresem funkcji (1.15) jest krzywa zwana krzywą wykładniczą, która przecina oś Oy w punkcie o współrzędnych (0,1).

Monotoniczność funkcji wykładniczej jest zależna od wartości podstawy a.

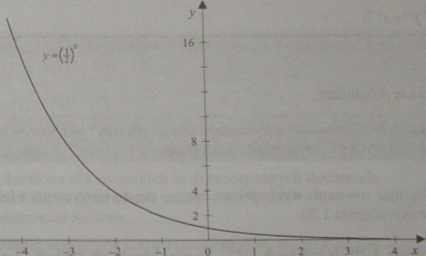
•    Dla a e (0,1) funkcja (1.15) jest malejąca w zbiorze liczb rzeczywistych (por. ilustracja 1.59).

•    Dla ae (l,co) funkcja (1.15) jest rosnąca w całej swojej dziedzinie (por. ilustracja 1.60).

Ilustracja 1.59. Wykres funkcji y = f i J