74708 PC043400

Zatem rozwiązanie równania »o połcgaiuwyziuKzaaiMi^. *ydł funkcji tywicnicj /i(i)«    .

Przykład 1.100

Wyrażenie wymierne    przyjmuje wartość 0 wtedy i tylko wtetS^

licznik tego wyrażenia będzie równy zero, a mianownik będzie oiezeroi^ r* + 4.r - 5 = 0 i .r + 2 * 0. Ponieważ rozwiązaniami równania kwidq^| x" + 4jr —5 = Osą liczby -5 oraz 1. spełniające warunekx * -2, są oocjofek elementami zbioru rozwiązań równania — = 0.

Nierówności postaci —j- >0,    >0, ~^<0 oraz    50, gdzie Vj|

są wielomianami oraz G(.v) * 0, nazywamy nierównościami wymiernymi Rozwiązywanie nierówności wymiernych sprowadzamy do rozwiąnug. nierówności wielomianowych, wykorzystując następujące równoważności.

•    %%^>0'»[iv(x)G(x)>0aG(x)*o],

•    ^ > 0 o [jK(:r) - G (*) > 0 a G (.v) * O],

•    ^<0o[«'(i)G(i)<0aG(i)*0],

•    ^soo[r(i).c(i)sOAGW*o],

Prawdziwość powyższych równoważności wynika z faktu, że znak flota dwóch liczb (wyrażeń) niezerowych jest taki sam jak znak ich iloczynu.

Przykład 1.101

Rozwiązanie nierówności    > 0 sprowadza się do rozwiązania nierór

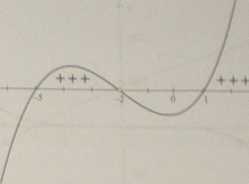
ności (x² + 4x- 5)(x + 2) > 0, przy warunku r + 2^0or#-2. Pierwiastki wielomianu (x² + 4x- 5)( x + 2) są liczby x_x - -5, x₂ = 1 orazx₃ ~ -2. Nar podstawie szkicujemy wykres tego wielomianu, pamiętając jednocześnie oi)“ że dziedziną nierówności jest zbiór R\{-2}.

Z ilustracji 1.54 odczytujemy, że (z² + 4x -5)(x + 2)2:0 ore [-5,-2]u[Ł*l Uwzględniając założenie, mamy -®^<=>xe [—5, -2) u[l, °o). ^

Preegląd tunkcji eleimmamych

|Q

Ilustracja I.M. SJfcic wykresu funkcji >■»* -u - 5)f* ♦ 2) dla t * -2

1.6.5. Funkcja potęgowa

Definicja 1.76. Funkcją potęgową zmiennej x nazywamy funkcję postaci:

gdzie ae R.

m=.v^a,

(1.14)

Własności funkcji (1.14) są zależne od wartości wykładnika a. Jeżeli:

•    wykładnik a jest liczbą naturalną dodatnią, to funkcja/(.v)=.v" jest szczególnym przypadkiem wielomianu, np. dla a = 5 mamy f(x) =r (por. ilustracja 1.55);

•    wykładnik a jest liczbą całkowitą ujemną, to funkcja potęgowa jest funkcją wymierną, której dziedziną jest zbiór R\{0}, np. dla a = -3 mamy f(x) »x , czyli f(x)=-jL (por. ilustracja 1.56);

•    wykładnik a = -£ (pe Z i qe N*) jest ułamkiem nieskracalnym, to funkcja (1.14) jest funkcją niewymierną i dodatkowo:

-    jeślipe Z* i <7 jest parzyste, toDy= (R⁺ u {0}, np. dla « = ■£■ mamy f(x) = .Y^:, czyli f(x) = -Jx (por. ilustracja 1.57);

-    jeśli pe Z* i q jest nieparzyste, toDy=R, np. dla a = -f mamy /(.v) = .v\ czyli f(x) = yjx⁵ (por. ilustracja 1.58);

-    jeśli p e Z" i q jest parzyste, to Dy = R\ np. dla a = —J mamy /(.v)» x *,

czyli/(*) i

-    jeśli pe Z~ i q jest nieparzyste, to Dy = R\{0}, np. dla a = —\ mamy

f(x)=x~*, czyli/(x) =    .