Strona0073

73

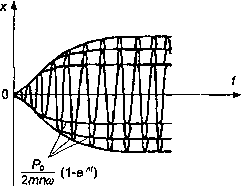
Rozwiązanie zależności (2.178) pokazano na rys. 2.33. Drgania ustalają się bez dudnienia, przy czym szybkość procesu zależy od wielkości tłumienia. Ob

73

wiednia

ustalone.

Po

2mno)

(1-e ^nt) stanowi granicę amplitudy, do której zmierzają drgania

2.10, Zadania do rozwiązania

z drgań punktu materialnego

Drgania swobodne Zadanie 2.1

Do sprężyny zamocowano ciało o masie m. Wychylenie statyczne sprężyny wynosi 5. Wyznaczyć równanie ruchu jc = x(t), jeżeli w chwili początkowej sprężyna była rozciągnięta ze stanu nienapiętego o 3t>, a ciało było puszczone bez początkowej prędkości.

Zadanie 2.2

Ciało o masie m = 0,1 kg zawieszono na końcu nieodkształconej sprężyny i puszczono bez początkowej prędkości. Długość sprężyny nieodkształconej wynosi 65 cm, a w położeniu równowagi z zaczepionym ciałem 85 cm. Wyznaczyć: równanie ruchu ciała, amplitudę i okres drgań, maksymalną siłę sprężystą.

Zadanie 2.3

Do końca sprężyny o stałej sprężystości k ~ 98 N/m podwieszono ciało o masie m = 2 kg. W chwili początkowej ciało znajduje się w położeniu równowagi i ma prędkość początkową v₀. Wiedząc, że amplituda drgań wynosi 2 cm, wyznaczyć wartość prędkości początkowej.

Zadanie 2.4

Sprężyna jest położona wzdłuż gładkiej równi pochyłej o kącie a. Jeden koniec sprężyny zamocowano u szczytu równi, na końcu nieodkształconej sprę-