ćw 2 wytrzymałość materiałów

-2-

Ćwiczenie 6

WYZNACZANIE STAŁYCH MATERIAŁOWYCH MATERIAŁÓW IZOTROPOWYCH METOD4 TENSOMETRYCZN4

Wstęp

Podstawowe obliczenia wytrzymałościowejprzeprowadza sij^na podstawie związków wyprowadzonych przy założeniu proporcjonalności odkształceń i naprężeń, co ^z\ dostatecznąjjiokładnością pokrywa się z doświadczeniem.^ We wzorach podstawowych praw wytrzymałości materiałów występują pewne wielkości noszące nazwę stałych materiałowych. W zależności od rodzaju materiału (izotropowy, ortotropowy, monotropowy itp.) liczba stałych materiałowych jest różna. Na przykład materiały izotropowe charakteryzują dwie niezależne stałe materiałowe^niezależne^Ąd_u.kł,adu_odniesi.enia. Są to moduł Younga - E i liczba Poissona - v> . W przypadku ciała ortotropo wego mamy do czynienia z dziewięcioma niezależnymi stałymi j^26J .

Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie modułu sprężystości podłużnej E 1 współczynnika Poissona V dla materiału izotropowego w zakresie odkształceń podlegających prawu Hooke a. Ćwiczenie przeprowadzamy dla przypadku jednoosiowego rozciągania przy wykorzystaniu techniki bezpośredniego pomiaru odkształceń tensometrem mechanicznym i elektrooporowym.

Podstawy teoretyczne

Materiały izotropowe chara.kt ery żują dwie niezależne stałe materiałowe B i V , natomiast inne stałe materiałowe ^wyrażone są w funkcji tych dwóch.

a) Współczynnik sprężystości podłużnej E - zwany modułem Younga (Thomas Young 1773-1823), występuje w podstawowym związku wytrzymałości materiałów - prawie Hooke a dla jednoosiowego rozciągania

| O = E • £ j    (1 >

gdziet

o - naprężenie normalne,

d - względne odkształcenie liniowe zgodne z kierunkiem obcia„że~ ni a.

Naprężenia normalne G wyznaczamy ze wzoru

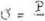
A

gdzie:

I- - siła. działająca, na. próbkę,

A - przekrój poprzeczny próbki.

Odkształcenie względne € wyznaczamy z relacji

£ =

Al

(3)

V

gdzie:

Al - przyrost długości,

1 - długość próbki przed odkształceniem.

b) Współczynnik Poissona. (Simeon Denis Poisson 1781-1840).    '    0 <1 \) L

Podczas rozciągania, pręta, występuje zjawisko zwężenia, przekroju poprzecznego, a przy ściskaniu spęczenie przekroju. Zachodzi przy tym proporcjonalność między wydłużeniami £ i poprzecznymi wydłużeniami £

£ A

V>= -

£

l\P

-

_s\>l

--£___J

U)

gazie:

v⁾- współczynnik proporcjonalności noszący na.zwę liczby Poissona. spełniający nierówność

1

(5)

c) Współczynnik sprężystości postaciowej G zwany modułem Kirchhoffa (Gustaw Robert Kirchhoff 1824-1887) występuje w prawie Hooke'a. czystego ścinania    i—(Ę

Wj ’±jjj \    f ^L

dla

(6)

A

gdzie:

X - naprężenia, styczne,

$ - kąt odkształcenia postaciowego.

Dla. materiałów izotropowych moduł Kirchhoffa można, wyznaczyć w leżności od modułu Younga i liczby Poissona. ze wzoru

G =

2(1+v»)

G

d) Współczynnik ściśliwości B - zwany modułem Helffiholtza (Herman Helmholtz 1821-1894) występuje w związku określającym prawo objętości

v = £    ,

(7)

Ludwik

zmiany

(8)

£T(IZ i 0 !

p - ciśnienie zewnętrzne> v - względne odkształcenie objętościowe.