0000020

28 Biomechanika kliniczna

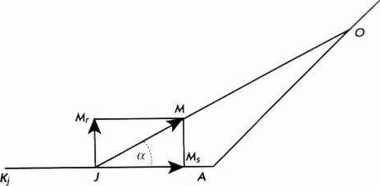
Ryc. 1. Działanie mięśnia na dźwignię kostną: K₀ - kość nieruchoma, O przyczep mięśnia początkowy, K, - kość ruchoma, J - przyczep mięśnia końcowy, O-A - odległość od początkowego przyczepu mięśnia do osi stawu, J-A - odległość od końcowego przyczepu mięśnia do osi stawu, a - kąt przyczepu. Lima łącząca przyczep początkowy i przyczep końcowy mięśnia oznacza kierunek działania siły mięśnia (wg [2])

obrotu), punkt przyłożenia siły oraz ramię siły, od którego zależy wielkość wektora siły mięśnia. Przyłożony do dźwigni kostnej wektor siły mięśnia kieruje się wzdłuż przebiegu ścięgna tego mięśnia, ponieważ to ono przenosi siłę mięśnia na dźwignię kostną (ryc. 1). Z rozkładu sił widać, że siła mięśnia nie działa całą swoją wielkością M w kierunku ruchu. W kierunku tym działa tylko składowa ruchu M_n ustawiona prostopadle do kości ruchomej. Druga składowa, M_s, działa w kierunku stawu A (zwierając go). Wielkość obu składowych jest zależna od kąta przyczepu a, utworzonego przez linię działania siły mięśnia w kierunku kości Kj. Im kąt a jest mniejszy, tym mniejsza jest składowa ruchowa M_r Wraz z ruchem kości Kj kąt a stale się zmienia, a wraz z nim wartość obu składowych.

Opis ten dotyczy warunków działania sił mięśniowych na sztywne, tj. nieruchome człony kostne. Dźwignia kostna jest (tak jak każda inna dźwignia) sztywnym członem (belką) podpartym w punkcie (osi) obrotu tak, że może się względem niego poruszać ruchem obrotowym. 0 ruchu obrotowym dźwigni decydują momenty sił (ryc. 2). Wielkość sity obrotowej mięśnia (M), działającego na staw (A) zależy od odległości linii działania siły mięśnia (O—J) od osi obrotu (A), tj. od ramienia siły (r_Af). Iloczyn siły skurczu mięśnia i ramienia siły nazywamy momentem siły mięśnia. Im dłuższe ramię sity' i im większa siła skurczu, tym większy jest moment siły.

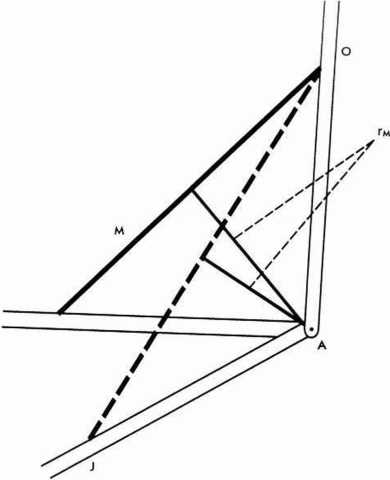
Ryc. 2. Moment siły: A - staw, M mięsień, O - przyczep początkowy mięśnia, J - przyczep końcowy mięśnia, r_M - ramię sity mięśnia (wg [2])

Aby dźwignia była utrzymywana nieruchomo w niezmienionym położeniu, muszą byc spełnione warunki równowagi. Zachowanie dźwigni w stanie równowagi jest możliwe dzięki zachowaniu równowagi momentów sił działających na dźwignię. Warunki utrzymania dźwigni jednoramiennej w stanie równowagi przedstawia ryc. 3.

4.2. Aktony i klasy mięśni

W opisie makroskopowym mięśnia uwzględnia się jego podział na brzusiec oraz ścięgna początkowe i końcowe. Często jednak poszczególne części tego samego mięśnia pełnią różne funkcje. Z tego więc powodu wyróżnia się tzw. akto-