0000066

w !

<° Oo X. zaliczony wierzchołki odpowiadaj«ce zerowym kolumnom w nowo powstałej eaciarry.

5° Powterzooy czynnotci 3° i 4° tworząc następne worotwy, oz do wyczerpanie całego zbioru wierzchołków digrafu (do wy-kreślenic ootatniego elementu macierzy P).

6.4. Grat Hertza

Ola dowolnego grafu [l7] lub hipergrofu G • <X.U,P,> określa mię unlgrof okierowany (digref) bez pętli, zwany grafem Hertza M(G)w naotępujęcy epooób

H(C) ■ <S. U^M. P^H>

gdzie i S Jeat zbiorem okładowych eilnej spójności grafu C,

U^H Jaat zbiorem luków u określonych naatępujtco

(i.,».,u^fl)£P^ ^ V f(X ■ ^ • • • • *|j #• • • •* _»• • • P ) A

^{1 J}    <,X,U>CP

A(x_kc a₁) A (x_#C Oj)]

W przypadku gdy G jeet grafem, to powyzozo zdanie moZna zopi -oać następująco

(a i u^h>(P^H ę=ę V [(<x,y.u>£P)A(xe»₁)A(yc»_J)]

^{1 J}    <M*X*    ^J

u tu

Przykład 8.2

wyznaczymy graf Hertza H(G) grafu G przedstawionego ne

rys.8.3.

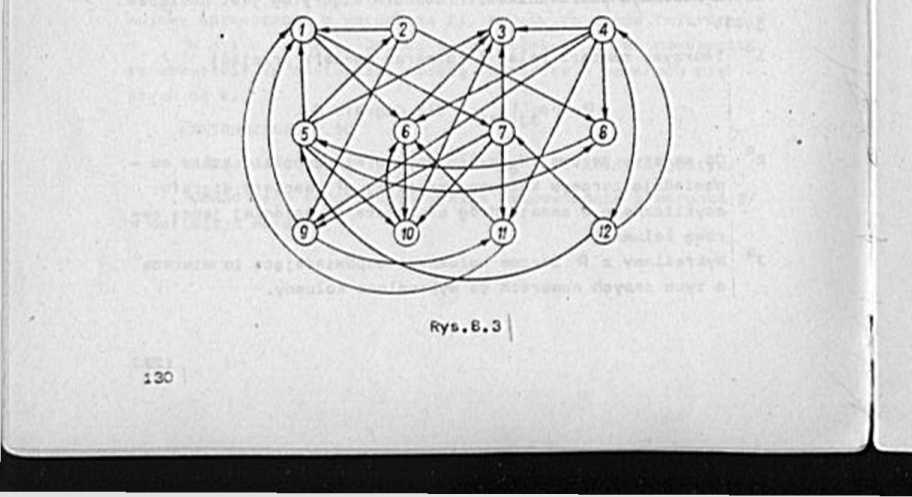
Macierz przojść togo grafu (macierz relacji) ma pootać

	1	2	3	4	5	6	7	6	9	10	11	12
1	0	0	0	0	0	1	1	0	0	0	0	0
2	1	0	0	0	0	0	0	1	1	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	0
4	0	0	1	0	0	1	0	1	1	0	1	1
5	1	1	1	0	u	0	0	1	a	1	0	0
6	0	0	1	0	0	0	0	0	0	1	0	0
7	0	0	1	0	0	0	0	0	1	1	1	0
6	0	0	0	0	1	0	0	0	0	0	0	0
9	1	0	0	0	0	0	0	0	0	0	1	0
10	0	0	1	0	0	1	0	0	0	0	0	0
11	1	0	0	0	0	1	0	0	0	0	0	0
12	0	0	0		1	0	1	0	0	0	0	0

Musimy najpierw wyznaczyć wezyetkle okładowe eilnej spójności grafu C za pomoce algorytmu Leifoana.

Roalizujgc punkt 1° algorytmu znajdujemy wierzchołek nr 3. który nie ma następników i tworzy pierwsze Jednowlerzchołkowe okładowy eilnoj spójności Sj - {3}.

Woźmy teraz jako x_Q wierzchołek nr 4. StosujfC procedurę cecho-wonla punktu 2° otrzymujemy X^ ■ {4,12}, X_l0 ■ 11,2,5,6.7,6, 9,10,ll} , X_Qł ■ JJ, X_Q0 ■ fS. Zatem druge okładowe tworzy zbiór

^S2 " {⁴'^ł2)»

Kyblerejec teraz w podgrafie, tworzonym przez zbiór wierzchołków X° • X₁q, wierzchołek poczetkowy do cechowania x_Q • 6, otrzymujemy X_n ■ (6.10) , X_łQ » fi. X_Ql • (l,2.5,7,8,9.11} ,

Xqq • p. Zatem trzecie okładowe tworzy zbiór X^ ;    • {6,10}.

Wybierajec x_Q ■ 5 otrzymujemy czwarte okładowe silnej spójności 1 ^S* . {2.5.8).

Pozootały zbiór wierzchołków {l,7,9,ll} w wyniku cechowania rozpoczętego, np. : od wierzchołka x_Q ■ 1, wchodzi cały do X_n, to znaczy etanowi piete okładowe ollnej spójności. ■ {l,7,9,ll}.

Przegledajfc teraz macierz przejść P(C) określamy relację P^H grafu H(C) -< S.U^H,P^M>

P • {<»2»*i*U$> ♦ <.*2'*3'^u2) • ^*2'^,4'^U3)

^*2'*5'^u4^ ' <*3'^łi*^u5> ' ^*4^,#3^,u6 ^

<*4.*1 ^,u7^ ' <^,4'ⁱ5'^u6> ' <^#5**i»^ug>

<®5*ⁱ3^,ulo)}

131