013 2

Funkcja liniowa

2)    układ nieoznaczony:

(W = 0 A W_X = 0 A w_v = 0) <r> ((3 - m)(m + I) = 0 a (4 - m)(m + 3) = 0 a a 3(w - 3) = 0)

m =5 3 v m = -1) a (m - 4 v m = -3) a m = 3 />? e 0

Nic istnieje takie nu dla którego układ ma nieskończenie wiele rozwiązań.

3)    układ sprzeczny:

(jf' = 0 a (IV # 0 v IV * 0)) o (3 m)(m + I) = 0 a [(4 - m)(ni + 3) * 0 v v 3(/;i - 3) * 0]

(ni = 3 v ;;/ = -1) a (w * 4 a m * -3 v m * 3) m = -1

Dla /;? = ^ 1 układ jest sprzeczny, czyli rozwiązaniem jest zbiór pusty. UKŁADY NIERÓWNOŚCI LINIOWYCH - przykładowe zadania

ZADANIE 1

Najpierw trzeba jedną i drugą nierówność uporządkować przez dokonanie zaznaczonych działań, a następnie przenieść niewiadome na lewą, a wiadome na prawą stronę.

Pamiętaj, że przy dzieleniu przez liczbę ujemną zmienia się znak nierówności na przeciwny.

.v + 4 > 2 - 3*

{4 (.v- 1)> 2 + lx

| x + 3.r > - 4 + 2 \4x-4> 2 + lx

[ 4x > -2 \ 4x ~lx> 4 + 2

4x > -2 /: 4 -3.r>6 /: (-3)

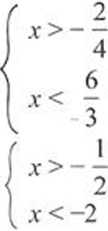
Teraz należy zilustrować otrzymane nierówności na osi liczbowej.

I 1-i—<•—i-i-►

-3    -2 -I 1 O    X

Szukamy części wspólnej przedziałów. Niestety, rozwiązaniem jest zbiór pusty.

Odpowiedź

X € 0

ZADANIE 2

Porządkujemy nierówności, przenosząc niewiadome na lewą stronę, a wiadome na prawą.

Uważaj na zmianę znaku.

3 + 5.v < lx + 4 \3jc-6<4jc-9

f 5x-7x<-3 +4 \ 3a* - 4.v < 6 - 9

( -2x < l /: (-2)

{-*<-3 !'• H)

x>-\
•i -! o : Odpowiedź .v e (3, +00)	*

Teraz ilustracja na osi liczbowej.

ZADANIE 3

7 - 6.v    8.v + l

——+ 12 <—---IO.y /• 6

Najpierw uwalniamy się od ułamków, mnożąc stronami nierówności przez odpowiednie liczby.

_    3.v-4    x-\ 5jc — 3 .

⁸⁺—^>T—T ^{/ l20}

25