img014

FUNKCJA PIERWOTNA, CAŁKA NIEOZNACZONA

Jeśli zaś funkcja/jest w przedziale I ciągła poza ewentualnie punktami, w których ma ona nieciągłość drugiego rodzaju, to / może, ale nie musi mieć funkcji pierwotnej w tymże przedziale (zobacz przykłady 2.2 i 2.3).

Reguły całkowania

Wprost z definicji całki nieoznaczonej oraz funkcji pierwotnej wynika, że jeśli funkcja rzeczywista /jest całkowalna w sensie Newtona w przedziale I <zR, to

(²-⁸)    ^Q/(*)d*) = Q7(*)<fc) =/(*),

gdzie różniczkowanie odnosi się do dowolnej funkcji pierwotnej/w przedziale /, zaś f(x) oznacza w tym przypadku funkcję/określoną w przedziale I, a nie —jak można sądzić — wartość funkcji / w punkcie x (zobacz też wzór (2.1)).

W sposób nie w pełni precyzyjny wzór (2.8) odczytujemy następująco:pochodna całki nieoznaczonej jest równa funkcji podcałkowej.

Twierdzenie 23 (o liniowości operatora całkowania nieoznaczonego)

Jeżeli funkcje rzeczywiste f i g są całkowalne w sensie Newtona w pewnym przedziale, to dla dowolnych liczb A, B e R funkcja Af + Bgjest również całkowalna w sensie Newtona w tymże przedziale, przy czym

(2.9)    j[A f(x)+B ■ g(x)]dx = A J f(x)dx +B jg(x)dx.

Uwaga 2.2

Znaki mnożenia i dodawania występujące po lewej stronie wzoru (2.9) odnoszą się do funkcji, po prawej stronie zaś — do klas funkcji (w tym przypadku do całki nieoznaczonej!). Korzystając z wcześniejszych definicji oraz ze wzorów na pochodne podstawowych funkcji elementarnych, otrzymujemy natychmiast następujące wzory podstawowe dla całek nieoznaczonych:

TABLICA 1

1.	x^a*' \x^adx=-- + C, gdy <x * -1 a +1
2.	f—= ln|jt|+C ^J X
3.	\a*dx =-+ C, gdya > Oia * 1 ^J Ina
4.	Jsin;n£t = -cosx + C
5.	Jcosxdr = sinx + C
6.	r dx 1.2= CtgX+C ^J sin x

—<^F+c, \tfxdx=—^r+c

n-1    ^J    n +1

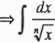
^7- J	2 -tgX+C COS X
8- .	dx „ , ■ — - arcsinx+ C yl\-X^2
^9‘ J	fl+jF ^=arctet+C

14