0008

10

VIII. Funkcja pierwotna (całka nieoznaczona)

Jeśli konkretnie dana funkcja ma punkty nieciągłości, to będziemy ją rozpatrywali tylko w przedziałach ciągłości. Dlatego zakładając, że spełnione jest wysłowione wyżej twierdzenie, nie musimy zastrzegać sobie za każdym razem istnienia całek: wszystkie rozpatrywane przez nas całki istnieją.

265. Tablica całek podstawowych. Każdy wzór rachunku różniczkowego orzekający, że pochodną pewnej funkcji F(x) jest /(x), prowadzi bezpośrednio do odpowiedniego wzoru rachunku całkowego

jf(x)dx = F(x)+C.

Na podstawie wzorów z ustępu 95, według których obliczaliśmy pochodne funkcji elementarnych, jak również niektórych wzorów wyprowadzonych później (dla funkcji hiperbolicznych) możemy ułożyć następującą tablicę całek:

1.    JO dx = C.

2.    J 1 •dx = J dx = x+C.

_    r*

3. JVdx = +C

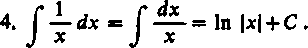
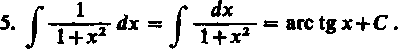
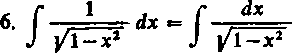
= arc sin x+C.

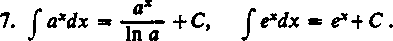
8.    J sinxdx = —cosx+C.

9.    f cosx dx = sin x+C.

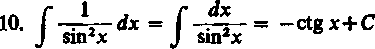
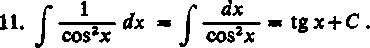
12.    J sinh x dx = cosh x+C.

13.    f cosh x dx = sinh x + C.

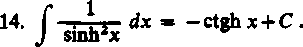
1

dx = tghx+C.

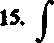
cosh²x