0060

62

VIII. Funkcja pierwotna (całka nieoznaczona)

Jeśli natomiast przy zmianie znaku u funkcja R (u, v) też zmienia znak, tzn. jeśli

R(-u,v) = -R(u,v),

to można ją sprowadzić do postaci

R (u, v) = R₂(u², v) u .

To ostatnie wynika od razu z poprzedniej uwagi, jeśli zastosować ją do funkcji R (u, v)/u.

I.    Niech teraz R (u, v) zmienia znak przy zmianie znaku u, wówczas

R (sin x, cos x) dx = £₀(sin²x, cos x) sin x dx = — R₀(l—cos² x, cos x) d cos x

i postać wymierną można osiągnąć podstawieniem t = cos x.

II.    Analogicznie, jeśli R (u, v) zmienia znak przy zmianie znaku v, to

R (sin x, cos x) dx = jR*(sin x, cos² x) cos x dx = R* (sin x, 1 — sin² x) d sin x ,

i do postaci wymiernej można dojść przez podstawienie t = sin x.

III.    Załóżmy wreszcie, że funkcja R (u, v) nie zmienia swej wartości przy jednoczesnej zmianie znaków u i v

R(-u, -v) = R (u, v) .

v

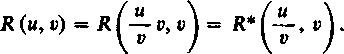
W tym przypadku pisząc zamiast u wyrażenie — v otrzymujemy

Z własności funkcji R wynika, że jeśli zmienić znaki u i v, to

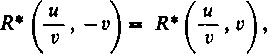
bo iloraz u/v nie zmienia się przy tym, a wówczas jak już wiemy, jest

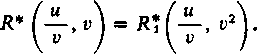
Dlatego

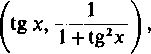
R (sin x, cos x) = R* (tg x, cos² x) = R*

tj. po prostu

R (sin x, cos x) = R (tg x) .