19763 P1111255

16 VIII. Funkcja pierwotna (całka nieoznaczona)

Przypuśćmy, że trzeba obliczyć całkę

W wielu przypadkach udaje się wybrać jako nową zmienną taką funkcję t = co (x) zmiennej x, żeby wyrażenie podcałkowe mogło być napisane w postaci f(x) dx = g (co (x)) co'(x) dx,

gdzie g (/) jest funkcją łatwiejszą do scałkowania niż f(x). Wtedy na mocy poprzedniego wystarczy znaleźć całkę

Jg(t)dt = G(t)+C,

aby przez podstawienie / = co (x) otrzymać z niej całkę szukaną. Zwykle piszemy po prostu

f f(x) dx= fg (t) dt,

rozumiejąc przez to, że w funkcji zmiennej t, wyrażonej całką stojącą po prawej stronie, wykonano już wspomniane podstawienie.

Obliczmy na przykład całkę

J sin³ x cos x dx.

Ponieważ dsin* = cosxdx_t więc podstawiając / = sin x przekształcimy wyrażenie podcałkowe do postaci

sin³ x cos x dx = sin³ x dsin x = t³ dt.

Całka ostatniego wyrażenia może być obliczona z łatwością:

jvd,=.ę₊c.

Pozostaje tylko powrócić do zmiennej x podstawiając sin x zamiast t

_r . ,    , sin⁴ x I

sin³ x cosx dx = —---hC.

J    4

Zwracamy uwagę czytelnika na to, że przy wyborze podstawienia t = co (x) upraszczającego wyrażenie podcałkowe trzeba pamiętać, że w jego skład musi wejść czynnik ©'(*) dx dający różniczkę nowej zmiennej, dt [patrz (I)]. W poprzednim przykładzie podstawienie t * sin :r było dogodne dzięki obecności czynnika cos xdx = dt.

W związku z tym interesujący jest przykład

| sin³ x dx.

Tu podstawienie f * sin x nie mogłoby być zastosowane właśnie ze względu na brak wspomnianego czynnika. Jeśli spróbować wyodrębnić z wyrażenia podcałkowego jako różniczkę nowej zmiennej czynnik sin x dx lub jeszcze lepiej, —sin x dx, to doprowadzi to do podstawienia t * cos x. Ponieważ wyrażenie, które pozostało,

—sin² x ** cos² x—1

upraszcza się przez takie podstawienie, podstawienie to może tu być użyte. Mamy

J sin³xdx p J yt²-\)dt *~-t+C ” -cos x+C.

Przy pewnej wprawie w wykonywaniu podstawień można nie pisać nawet zmiennej t. Na przykład w całce

J sin³ x cos xdx — J sin³ x d sin x

można w pamięci traktować sin x jako nową zmienną i od razu otrzymać wynik. Analogicznie

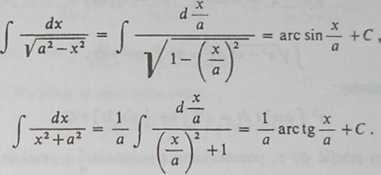
Przeprowadzamy tu w pamięci podstawienie t = x/a.

Czytelnik widzi teraz, że reguła 111,266 sprowadza się właściwie do podstawienia liniowego t «* ax+b:

C f(ax+b)dx = ~ J* f(ax+b) d (ax+b) =    .

Niekiedy używa się podstawień w inny sposób niż pokazany wyżej. Podstawia się mianowicie za x do wyrażenia podcałkowego f{x)dx bezpośrednio funkcję x =» ?(/) nowej zmiennej t i otrzymuje się w wyniku wyrażenie

/(? (0)p'(0* = g(t)dt.

Jeśli w tym wyrażeniu dokonać podstawienia t = co (x), gdzie co (x) jest funkcją odwrotną względem? (/), to powrócimy oczywiście do wyjściowego wyrażenia podcałkowego/(.v) dx. Zachodzi więc, jak i w poprzednim wypadku, równość (2), gdzie po prawej stronie po obliczeniu całki — trzeba podstawić / *= co (x).

Obliczmy na przykład całkę

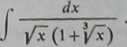
Jeśli podstawimy x = t⁶ (żeby dały się wyciągnąć wszystkie pierwiastki), to otrzymamy fi/x * f³, {/i = i¹* dx = 6t*dt i