P1111260

26 VIII. Funkcja pierwotna (całka nieoznaczona)

Otrzymany wzór sprowadza obliczenie całki /_R+j do obliczenia całki /„ ze wskaźnikiem o jeden mniejszym. Znając całkę

J_t *= — arc tg —

a    <7

[267,9) (b); bierzemy jedną z jej wartości] znajdziemy według tego wzoru dla « = 1

/i -

_!---*__ ₊ _L-_arctgJ:,

2n^ł j:^a+fl^a 2o³    a co otrzymaliśmy wyżej inną drogą fp. 269.8)]. Biorąc we wzorze (6)n — 2 otrzymujemy następnie

----i--- — --1—— arc tg —

4o²    (.v²+n²)²    8n⁴    .v²+o²    8n⁵    r/

A =

3

4o² (z^a+n^a)^a 4n^a itd. W ten sposób można obliczyć całkę/* dla dowolnego n naturalnego.

§ 2. Całkowanie funkcji wymiernych

272. Sformułowanie zagadnienia o całkowaniu w postaci skończonej. Zapoznaliśmy się z elementarnymi sposobami obliczania całek nieoznaczonych. Sposoby te nie wyzna*; czają dokładnie drogi, po której należy pójść, aby obliczyć daną całkę, pozostawiając wiele umiejętnościom obliczającego. W tym i następnych paragrafach zatrzymamy się; dokładniej na pewnych ważnych klasach funkcji i dla ich całek ustaliny zupełnie określony schemat obliczeń.

Wyjaśnimy obecnie, co mianowicie będzie nas interesowało przy całkowaniu funkcji! wspomnianych klas i na jakiej zasadzie wyróżniamy te właśnie klasy.

W ustępie 51 scharakteryzowaliśmy zbiór tych funkcji do których w pierwszym rzędzie stosuje się analiza. Są to tak zwane funkcje elementarne i funkcje, które mogą być wyrażone przez nie za pomocą skończonej liczby działań arytmetycznych i superpozycji bez stosowania przejścia do granicy.

W rozdziale III widzieliśmy, że wszystkie takie funkcje są różniczkowalne i ich pochodne należą do tego samego zbioru. Inaczej ma się sprawa z ich całkami; bardzo często okazuje się, że całka funkcji należącej do wspomnianej klasy, sama do tej klasy nie należy, tzn. nie wyraża się przez funkcje elementarne za pomocą skończonej liczby wymienionych wyżej operacji. Do takich całek, na pewno nie wyrażających się w postaci skończonej, należą na przykład całki

J cos x²dx,

J dx, J sin x² dx,

Należy podkreślić, że wszystkie te całki istnieją realnie ('), są to tylko zupełnie nowe funkcje i nie sprowadzają się do tych funkcji, które nazwaliśmy funkcjami elementarnymi (²).

Znane są stosunkowo nieliczne ogólne klasy funkcji, które mogą być scałkowane w postaci skończonej, klasami tymi zajmiemy się obecnie. Na pierwszym miejscu wśród nich należy postawić ważną klasę funkcji wymiernych.

273. Ułamki proste i ich całkowanie. Ponieważ z ułamka wymiernego niewłaściwego można wyłączyć część całkowitą, której całkowanie nie przedstawia trudności, wystarczy zająć się całkowaniem ułamków właściwych, tzn. takich, w których stopień licznika jest niższy od stopnia mianownika.

Spośród nich rozpatrzymy tutaj tak zwane ułamki proste. Będą to ułamki następujących czterech typów:

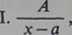
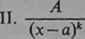
(* = 2,3,...),

x²+px+q ’

{x² + px+q)T

fil.

_iy Mx+N

(m = 2, 3,...),

gdzie A, M, N, a, p, q są liczbami rzeczywistymi. Oprócz tego zakładamy, że trójmian x²+px+q w ułamkach typu III i IV nie ma pierwiastków rzeczywistych, a więc

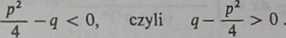
Ułamki postaci I i II umiemy [267,7)] już całkować:

Co się zaś tyczy ułamków postaci III i IV, to całkowanie ich upraszcza się przez następujące podstawienie. Wydzielamy z wyrażenia x²+px+q pełny kwadrat dwumianu

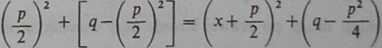
x²+px+q = x²+2 ^mx+

Ostatnie wyrażenie w nawiasie jest zgodnie z założeniem liczbą dodatnią równą a², jeśli przyjąć

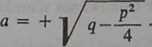
C) Patrz, co mówi się o tym w ustępie 264 Powrócimy do tego niżej, w ustępie 305. (^a) Aby pomóc czytelnikowi oswoić się z tym faktem, przypominamy, że całki

f dx f dx

J x 1 J 1+**

funkcji wymiernych same już nie są funkcjami wymiernymi. Gdyby więc „elementarnymi'* funkcjami były dla nas funkcje wymierne, to już wymienione całki funkcji „elementarnych” nie wyrażałyby się przez funkcje „elementarne”, lecz byłyby funkcjami „nieelementarnymi” nowego rodzaju — In * i arc tg.t.