21923 P1111252

10 VIII. Funkcja pierwotna (całka nieoznaczona)

Jeśli konkretnie dana funkcja ma punkty nieciągłości, to będziemy ją rozpatrywali tylko w przedziałach ciągłości. Dlatego zakładając, źe spełnione jest wysłowione wyżej twierdzenie, nie musimy zastrzegać sobie za każdym razem istnienia całek: wszystkie rozpatrywane przez nas całki istnieją.

265. Tablica całek podstawowych. Każdy wzór rachunku różniczkowego orzekający, że pochodną pewnej funkcji F(x) jest /(x), prowadzi bezpośrednio do odpowiedniego wzoru rachunku całkowego

jf(x)dx =■ F(x)+C.

Na podstawie wzorów z ustępu 95, według których obliczaliśmy pochodne funkcji elementarnych, jak również niektórych wzorów wyprowadzonych później (dla funkcji hiperbolicznych) możemy ułożyć następującą tablicę całek:

1.    J"0<ix«C.

2.    J = J dx = x+C.

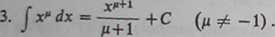
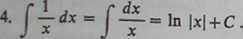
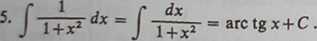
1

‘I

= arc sinx+C.

</*=/•

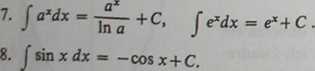
9. Jcosxdx « sinx+C.

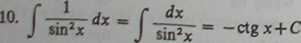
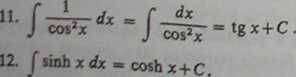
13. Jcosb x dx m sjnh x+ ę.

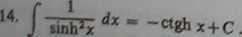
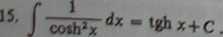
Wzór 4 wymaga pewnego objaśnienia. Może on być stosowany w dowolnym przedziale nie zawierającym zera. Rzeczywiście, jeśli przedział ten leży na prawo od zera, a więc

x > 0, to ze znanego wzoru [ln x]' = — wynika bezpośrednio, że

J£ = ln*+C.

Jeśli natomiast przedział leży na lewo od zera, a więc x < 0, to różniczkując możemy się łatwo przekonać, że [ln(—x)y = —, skąd

/£ = ,„(—_x)+c

Oba te wzory połączone razem dają wzór 4.

Wprowadzenie reguł całkowania pozwoli nam rozszerzyć możliwość znajdowania całek.

266. Najprostsze reguły całkowania

I.    Jeśli a jest stalą (a # 0), to

f a ’f (x) dx = a • j f{x) dx.

Rzeczywiście, różniczkując wyrażenie stojące po prawej stronie otrzymujemy [105,1]:

d \a f f(x) dxj = a • d J jf (x) dxj = a /(x) dx,

a. więc jest to funkcja pierwotna wyrażenia o-f(x) dx, c.b.d.o.

Tak więc czynnik stały można wynosić spod znaku całki.

II.    J [f(x)±g (x)] dx = J/(x) dx± f g (x) dx.

Różniczkujemy wyrażenie stojące po prawej stronie [105,11]:

d | J m dx±fg (x) dxj = d jf(x) dx±d Jg (x) dx = [f(x)±g (x)] dx\

jest ono więc funkcją pierwotną ostatniej różniczki, c.b.d.o.

Całka nieoznaczona sumy (różnicy) różniczek równa się sumie (różnicy) całek każdej z różniczek z osobna.

Uwaga. W związku z dwoma powyższymi wzorami zauważmy rzecz następującą. We wzorach tych występują całki nieoznaczone, z których każda zawiera stałą dowolną. Równości tego typu rozumiane są w tym sensie, że różnica prawej i lewej strony jest stała. Można również traktować takie równości dosłownie, lecz wówczas jedna z występiyących w nich całek przestaje być dowolną funkcją pierwotną: jej stałą wyznacza się po wyborze stałych w pozostałych całkach. O tej ważnej uwadze trzeba pamiętać na przyszłość.