P1111258

22

VIII. Funkcja pierwotna (całka nieoznaczona)

Przyjmijmy y'x²+oc —

dukując otrzymamy

/—jvi weźmy t jako nową zmienną. Podnosząc obustronnie do kwadratu i re-

2/

a więc

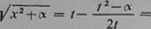
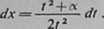
Ostatecznie

——= /*—— In l/l-ł-C* — ln|*+/*^J+a|+C

jfplpl p |

[por. 9]

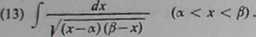
Podstawmy * «= acos³p+flsin²p (0<9>< -j-rc), gdzie <p jest nową zmienną. Wówczas x—a «= (fi—<x) sin* ę>, p—x = (fi—a) cos^aę>, dx = 2 (fi—») sin ę> cos .

\f(x-<x)(fi-x)

Tak więc

270. Całkowanie przez części. Niech u—f(x) i u — g (x) będą funkcjami x mającymi ciągłe pochodne u * f(x) i o' — g'(x). Wówczas na mocy reguł różniczkowania d (ud) = =udv+vdu lub udo — d(uo)—vdu. Funkcją pierwotną wyrażenia d(uv) będzie oczywiście ud, zachodzi więc wzór

(?)

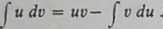
Wzór ten wyraża regułę całkowania przez części. Sprowadza on całkowanie wyrażenia u do = uv'dx do całkowania wyrażenia o du — vu'dx.

Obliczmy na przykład całkę x cos x dx. Przyjmujemy

u = x, do = cos x dx, a więc du — dx, v = sin x (*).

na mocy wzoru (3) jest

(4) j x cos x dx = J x d sin x = x sin x— J sin x. dx = x sin x+cos jc+C .

Tak więc całkowanie przez części pozwoliło nam zastąpić skomplikowaną funkcję podcałkową x cos x przez prostszą funkcję sin x. Jednocześnie, aby otrzymać u, trzeba było scałkować wyrażenie cos x dx. Stąd bierze się nazwa całkowanie przez części.

Stosując wzór (3) do obliczania danej całki, musimy rozbić wyrażenie podcałkowe na dwa czynniki u \ do - v'dx, z których pierwszy różniczkujemy, a drugi całkujemy przy przejściu do całki znajdującej się po prawej stronie. Należy się postarać o to, aby całkowanie różniczki do nie sprawiało trudności i aby zamiana u na du i do na u prowadziła

(') Ponieważ cel, do którego dążymy może być osiągnięty, gdy potrafimy przedstawić cosxdx w postaci do choćby na jeden sposób, nie ma potrzeby pisać dla v najogólniejszego wyrażenia zawierającego stałą dowolną. Należy o tym pamiętać dalej.

§ 1. Całka nieoznaczona i najprostsze sposoby jej wyznaczania

23

ostatecznie do uproszczenia wyrażenia podcałkowego. Tak na przykład w rozpatrywanym przykładzie byłoby, jak widać, niewygodnie przyjąć xdx za dv, a cos x za u.

Przy pewnej wprawie nie trzeba wprowadzać oznaczeń u, t>, można od razu zastosować wzór [por. (4)].

Reguła całkowania przez części ma mniejsze zastosowanie niż całkowanie przez podstawienie. Istnieją jednak klasy całek, na przykład

J x^kln"x dx, j sin bx dx, f x* cos bx dx, J x*e"dx

i inne, które obliczamy właśnie za pomocą całkowania przez części.

Powtórne zastosowanie reguły całkowania przez części prowadzi do tak zwanego uogólnionego wzoru na całkowanie przez części.

Załóżmy, że funkcje u i v mają w rozpatrywanym przedziale ciągłe pochodne wszystkich rzędów do n + 1 włącznie: u\ v\ u"> v'_t..., u⁰⁰, p⁽"\ u⁽"⁺¹⁾,    .

Podstawiając do wzoru (3) zamiast v wyrażenie v^M otrzymujemy

Analogicznie

/

li

dv^M = uv^M- j v^wdu = uv^iH}

dx.

j u'o^M dx = ttV-¹> - fu" dx, J _u"o<*-ⁱ>dx = _u"v⁽"-²⁾— J u"V"-²⁾ dx

J u⁽"V dx = u^wo— J u^{H+^v dx.

Mnożąc te równości kolejno przez +1 lub — 1 i dodając je stronami otrzymujemy po redukcji jednakowych całek po obu stronach równości wzór

(5)    j uo⁽"⁺¹⁾ dx = tin⁰⁰ — uV"^_1)+u^/V"“²⁾— ... +(— iy^,u^wv+{— l)"*¹ J u^im*^l)vdx.

Szczególnie wygodny jest ten wzór wówczas, gdy jednym z czynników jest wielomian algebraiczny. Jeśli u jest wielomianem stopnia n, to u^(H+l) jest równe tożsamościowo zeru i dla całki znajdującej się po lewej stronie równości otrzymujemy ostateczny wynik. Przejdźmy do przykładów.

271. Przykłady 1) fx³lnxdx.

Różniczkowanie lnx prowadzi do uproszczenia, przyjmujemy więc

u = In x, do — x*dx, a zatem du = —, v — -j- x*,

x    ⁴

f x³ In x dx = ~ x⁴ In x— 4 f x³dx — k x⁴ In x— -J- x*+ C. 2) (a) J ln x dx, (b) f arc tg x dx, (c) j arc sin x dx.

Przyjmując we wszystkich przypadkach dx g do otrzymujemy

(a)    flnxdx — xlnx— f xdlnx == xlnx— f dx = x(lnx— 1)+C;

(b)    j arc tg x dx = x arc tg x— J x rfarc tg x — x arc tg x— J —j— dx «**

(p. 269,5) (a)J;

— x arc tg x— ~ In (x^ł +1).+ C