012

Funkcja liniowa

1)    układ oznaczony:

IV *()<=> 4- nr * 0 (2 - ///)(2 + ///) 0

^ 2 a m * -2

Dla /;/ g R \ {-2, 2} układ posiada dokładnie jedno rozwiązanie postaci:

W_x 12-6/w _    6 O^r)    6

fF    4 - nr    (Z^rff)(2 + tu)    2 + m

W_r = 6 - 3w ₌    3(23

FF    4 - wr    (2^tźT)(2 + m) 2 + m

2)    układ nieoznaczony:

(IV = 0 a JF = 0 a JF = 0) o (4 - nr - 0 a 12 - 6m = 0 a 6 = 3w = 0)

(2 - ///)(2 + m) = 0 a 6(2 - m) = 0 a 3(2 - m) = 0 (/;/ -2 v /?? = -2) a /// = 2 a w = 2 Zatem rozwiązaniem tych warunków jest w = 2.

Dla ni = 2 otrzymujemy: W = lf \ = JF 0, tak więc układ ma nieskończenie wiele rozwiązań i ma postać:

x + 2y = 3 2.v + 4 v = 6

3)    układ sprzeczny:

(iv= 0 A (»; *0v)N 0)) o (4 - nr= 0 A (12 - 6m ^0v6 = 3»i/0)) (ni = 2 v /;/ = ~2) a (ni * 2 v ni * -2)

(ni = 2v/»a -2) a /;/ * 2 Widzimy, że jedynie /;/ = -2 spełnia te warunki.

Dla = 2 otrzymujemy: JF = 0, JF = 24, JF = 12, zatem układ jest sprzeczny. Zbierzmy teraz otrzymane wyniki:

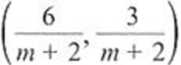
• jeżeli ni e R\ {-2, 2} to układ spełnia para liczb

• jeżeli ni = 2 to układ spełnia nieskończenie wiele par liczb rzeczywistych

• jeżeli /;; = -2 to układu nie spełnia żadna para liczb (rozwiązaniem jest zbiór pusty).

ZADANIE 2___

Rozwiąż układ równań liniowych:

f (w - 2)x - 3v = m + 1 [ x - my - 4

Przeprowadź dyskusję rozwiazalności tego układu ze względu na parametr m.

Rozwiązanie:

Obliczymy wyznaczniki IV. IV , IV

-3

m - 2

W =

W =

W =

V

1

-ni

/;/ + 1    -3

4    - m

m - 2 m + 1

1    4

= (ni - 2) • (-///)- (-3) • 1 = -nr + 2m + 3 = (3 - /;/)(/;/ + I)

= (/;/ + I) • (-///)- (-3) • 4 = -nr - m + 12 = (4 - m){m + 3)

= (m - 2) • 4 {ni + !)•! = 4/;; - 8 - m - 1 = 3/;; - 9

1- 12    3/// - 9    3(w - 3)    3

-nr + 2m + 3    - nr + 2m + 3 - (m - 3)(m + 1)    /// + 1

1) układ oznaczony:

IV #()<=> —nr + 2m + 3*0 (3-w)(w + I)* o /;; * 3 a /// * -1

Dla me R \ {-1, 3} rozwiązaniem jest para liczb postaci:

-nr-m+ 12 .    3

-nr + 2m + 3 * *'    m + 1

23