53 (134)

3.1. Funkcjo liniowa

3.1.6. Układy równań liniowych i parametrem

Oznaczenia: x,y- niewiadome k - parametr

/,(* ),£,(*)•    *) “ funkcje parametru k w roli współczynników

(odpowiednio a₍, b_v c₍) układu (i = 1,2)

/i(*)#⁺*i(*)?^ts/,i(*)

Mogą zaistnieć trzy następujące przypndki w zależności od wartości wyznaczników:

/,(*) *.(*)

/»(*) ■

W_ =

*,(*) *.(*)

*j(*)    *₂(*)

H'.=

pi Ili

/:(*) ■

W=

I	II		111
Układ oznaczony	Układ nieoznaczony			Układ sprzeczny
(układ równań niezależnych),	(układ równań zależnych),		(układ równań s		p rzecznych),
gdy		gdy		gdy
W#0.		W=0		W=0	W= 0
Wówczas istnieje jedno		Wx = 0 = Wy'		V jHpl	wy*o-

rozwiązanie W.

Wówczas istnieje nieskończenie wiele rozwiązań.

Wówczas brak rozwiązań.

W •

^yo⁼ w

Układ nie ma rozwiązań

Układ ma rozwiązanie Każde z równań przedstawia pewną prostą na płaszczyźnie:

Graficznie proste przecinają się. Graficznie proste pokrywają się. Graficznie proste są rozłączne.

Proste są równoległe

Powyższe przypadki można ująć w następujący schemat:

= °

(możliwe dwa przypadki)

LŁS

\*0 W'^y0 wl

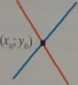
Układ oznaczony

Układ nieoznaczony W_x=0 = W_y

Układ sprzeczny W* 0 V

m

Na przykład:

Rozwiązanie istnieje

Proste są równolegle

{(*+ l)* + 3y= 1	k +1 3 I 2	1 3		k+1 1
l* + (k-l)y=-l’ |.^=	1 k-\ = ^k~^4’ ^W'^m	-1 k - 1	= k+ 2, Wy =	ł -1	= -k-2

1 ^k*^± 2 Ml układ ma jedno

k-2

- jest oznaczony.

rozwiązanie:

k-2

y =

Dla*    ⁼ W,= W ) układ ma nieskończenie wiele rozwiązań - jest nieoznaczony.

_____~ (tylko W = 0) układ nie ma rozwiązuń - jest sprzeczny.