0316

będą względem siebie równoległe. Wtedy przez zwój przechodzić będzie największy strumień O indukcji zewnętrznej B₀ i własnej B' (ryc. 17.13).

Elektron o ładunku —e poruszający się po orbicie atomu (ryc. 17.12) z częstotliwością v, |Ub z prędkością v, przedstawia prąd kołowy o natężeniu

Moment magnetyczny tego prądu wynosi

Pm

= IS = - e

v

2 tz r

-r-

1

~2~evr

17.29

Elektron o masie m krążąc po orbicie o promieniu /• z prędkością v ma również mechaniczny moment pędu (orbitalny), wyrażony wzorem

Ryc. 17.12. Moment magnetyczny p,„ i orbitalny moment prądu L elektronu.

L = mvr    17.30

L jest wektorem prostopadłym do r i v o zwrocie zgodnym z regułą śruby prawoskrętnej, a więc przeciwny do wektora u., ponieważ zwroty ruchu elektronu i prądu elektrycznego są przeciwne. Ze wzorów 17.30 i 17.31 wynika, że stosunek wartości liczbowej orbitalnego momentu magnetycznego elektronu do wartości jego momentu pędu wynosi

17.31

Nie zależy on ani od prędkości elektronu na orbicie, ani od promienia orbity. W modelu atomu Bohra na pierwszej orbicie L — h. Uwzględniając to we wzorze 17.31 mamy

Pm

eh

1m

= 9,27 • 10 ²⁴ Am²

Ta wartość momentu magnetycznego nosi nazwę magnetonu Bohra [j._B. Wzór 17.31 można zapisać wektorowo

Pm

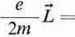
— gL

gdzie: g = -i oznacza orbitalny współczynnik giromagnetyczny.

Im

W atomach, w których jest Z elektronów, orbitalne momenty magnetyczne sumują się wektorowo i dają orbitalny moment magnetyczny całego atomu

z

Pm_a ~ LjPmi

i— l

Zewnętrzne pole magnetyczne, działając na dipole magnetyczne atomów próbki momentem obrotowym T (wzór 17.28), usiłuje ustawić je tak, aby p_m i B₀ były do siebie równolegle. Przeszkodą na drodze do pełnego uporządkowania dipoli atomowych są chaotyczne

322