039 3

Zadania dodatkowe

,v > 2 x<4 x< 13

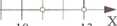
4    6    i u    u

Ostatecznie x e (2, 4).

Teraz rozwiązujemy równanie

log (x - 2) - log (4 - x) = 1 - log (13 - ,v) log (x - 2) - log (4 — a-) = logi 0 — log (13— ,y)

logarytmy są dziesiętne, dlatego 1 = Iog10

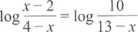
Korzystamy ze wzoru

x —2 _ 10    _b

4-Tic ~TJ-jc    Hd-io_g/=io_gł-

(podstawy logarytmów są równe, dlatego porównujemy liczby logarytmowane)

Równanie to rozwiązujemy, mnożąc wyrażenia „na krzyż’’

(jc — 2)( 13 —jc) = 10(4 -.y)

13.y-y²-26 + 2jt = 40-10.r    a c    _h

j — j czyli a ■ d = b • c

13x - jt² - 26 + 2y 40+ 10.y = 0 -a-² + 25,y - 66 = 0    /-(-l)

^-25*+ 66 = 0    a= 1, 6 =*.-25, c= 66

A = b² - 4ac = (—25)² -4 1 - 66 = 625 - 264 = 361 = V36l= 19

-b-<A 25- 19 6 ,

^s---2—r³

~/> + Va 25 +19 44 „„

—T"²²

Sprawdzamy, czy znalezione liczby 3, 22 należą do dziedziny równania.

Tylko 3 należy i jest zarazem liczbą b Czyli

b = 3

Wyznaczyliśmy zatem przedział [a, 6], Jest nim przedział [2, 3],

Zgodnie z warunkami zadania granica ciągu (bj ma należeć do tego przedziału, czyli

Pil

2

[2₍ 3]

Oznacza to, że liczba ta -równa 3.

£11

2

jest większa lub równa 2, a mniejsza lub

2 < -

Pil

2

<3

/ • 2

4 < — (p + 5) <6

Zapisując powyższe nierówności inaczej uzyskujemy układ

( ~(p + 5) < 6    /-(-l)

\ ~(p + 5) > 4    /-(-l)

f (j> + 5) > -6 \ (P + 5) < -4

\p>-5~6

\p<-5-4

{p>-\\

\p<-9

Zapisując układ inaczej, mamy 11 <p<-9 Czyli p e [-11, -9]

Odpowiedź

Dla p e [-11,-9] granica ciągu (b_n) jest liczbą z przedziału [2, 3].

ZADANIE 16_

Dla jakich wartości parametru m dziedziną funkcji j\x) = log [(2ni - 3).v- + (6 - m)x + y (m - 9)] jest zbiór wszystkich liczb rzeczywistych?

77