033 2

Zadania dodatkowe

Zadania dodatkowe

aby rozwiązać taką nierówność, trzeba ją zlo-garytmować stronami, logarytmem o podstawie 2, wtedy bardzo łatwo uzyskać x. bo logy - x

log,2' < log,9 x < log,9

D/icdzina równania: ( oo, log,9)

Rozwiązanie:

log,(9 - 2^V) = 3 x

2^3_Jf = 9 - 2*

Korzystamy z definicji logarytmu log_6 ■ *o a* *= b

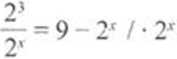
Korzystamy ze wzoru: a^{1 1} ~

<v

t-

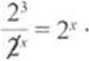
9

2' • 2*

2³ = 9 • 2* - 2^lv

8 = 9- 2 \- 2^2v

Korzystamy ze wzoru 2ⁱ = 8

8 - 9 • 2^T + 2²* = 0 2^lx - 9 • 2^V + 8 = 0 Podstawiam 2^X = t, / > 0 l² - 9/ + 8 = 0

A = (-9)--4* 1-8 = 81 -32=49 >/a = >/49 = 7

Teraz trzeba rozwiązać równanie wykładnicze metodą podstawiania.

Przenoszę wyrażenia na lewą stronę, porządkuję równanie

2^U = (2 ‘Y = 0, ze wzoru (a*V = a" ^r a = 1, ó = -9, c = 8

Teraz trzeba rozwiązać równanie kwadratowe, licząc A i pierwiastki

A = JP- 4jc

. -b + NA

^r'*~25~

Teraz wracamy do podstawienia, aby uzyskać x

2 ' = t

czyli

2-/,= l	lub	2^X
2^X = 1	lub	V

2‘ = 2°    lub    2' = 2'

.v = 0    lub    ,v = 3

Sprawdzamy, czy znalezione liczby należą do dziedziny (tak!)

Odpowiedź

.v = 0 lub x =3

ZADANIE 11_ _

Rozwiąż równanie:

log73 - Ioj»(.y-' - 1) = 3Io«2 - IogA - log(.v - 1)

Dziedzina równania:

(y -1	>0
x > 0
lv- 1	>0
(x^x > 1	stąd	’ X > 1
{x > 0	stąd	.V > 0
Iy> 1	stąd	Lv > 1
nr
0	T- 1	X

Dziedziną równania jest zbiór (I, + x). czyli I): x e (1. +cc)

Rozwiązanie:

log73 - log(.v³ - 1) = 3log2 - log.Y - log(.v - 1) log73 - log(.v³ - 1) = log2³ - logv - log(.v - I)

Korzystamy ze wzorów:

log    = log - - log (.V - I)    109/-109/ - 109.p

■'    •'    log;b* = x -log^ó

^    Znowu korzystam ze wzoru:

^lo2 | ~ ^,02 _x{~ ,₎    log/-log,/ = log,*

Teraz, skoro logarytmy mają tę samą podstawę i są równe, opuszczam znak Jog", porównując tylko liczby logarytmowane.

65