042

Zadania dodatkowe

Teraz rozwiązujemy nierówność w dwóch przypadkach I

{.V e (0, 1)    wówczas funkcja logarytmiczna jest malejąca

!og_r(.Y + 2) < log A-'

x + 2>x* x +2-x² > 0

x c (0,1), zatem opuszczając logarytm zmieniamy znak na przeciwny

- x² + .v + 2 > 0    /-(-l)

.y^: -.v - 2 < 0    a=1>-1,f*-2

A = /r - 4ac = (-1 )² - 4 • 1 • (-2) = 1+8 = 9

vS = 3

x.

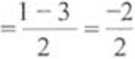
= -l

1+34 2 "2

lub

2

v.

Teraz pomocniczy rysunek

Znajdujemy część wspólną otrzymanego zbioru ( 1, 2) i zbioru wyznaczającego pierwszy przypadek (0. I):

-ę----1—►y

-10 12 ^A

R: x € (0. 1)

Część wspólna jest zbiorem (0, 1).

f.Y € (1, +CC)

\ log_v(.v + 2) < log/²

W tym przypadku funkcja logarytmiczna jest ro snąca

.v + 2 < .v^:

,v + 2 - X² < O

-x² + jc + 2<0    /•(-!)

X² - .v - 2 > O

A = /r - 4ac = (^_ 1)^: - 4 • 1 -(-2) = 9 a/A = 3

x € (1, + x), zatem opuszczając logarytm nie zmieniamy znaku nierówności

a = 1, b = -1, c = -2

-b - \A	1-3	_2
^A,_ la	2	2
-b + \'A	1+3	.-i- 2
2a	2	2 ^2

Teraz pomocniczy rysunek

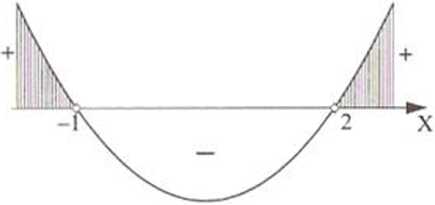
x € (-00,-1) u (2,+00)

Znajdujemy część wspólną otrzymanego zbioru (-cc, -1) u (2. +cc) i zbioru wyznaczającego pierwszy przypadek (1, +oc):

x e (2, +cc)

.v e (—cc, —1)	X € (1, +>0)
V-1-V-1-V- -10 1 2

R: x e (2, +*>)

Otrzymany zbiór jest rozwiązaniem nierówności dla drugiego przypadku. Rozwiązaniem nierówności jest suma rozwiązań dla obu przypadków.

83