044 2

Zadania dodatkowe

Teraz pomocniczy rysunek

Zadania dodatkowe

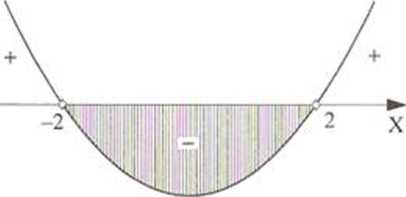
.V 6 (-2, 2)

Szukamy części wspólnej znalezionego zbioru i dziedziny

Zbiór:    x e (-2, 2)

Dziedzina: x e (-cc, - l)u(l, +x)

Część wspólna

x € (-oo,-i)				.V€(l,+O0)
!
	-2 -		v- 1 2

R: x e (-2, -1) u (1, 2)

Odpowiedź

Rozwiązaniem nierówności jest zbiór (-2. - I) u (1,2)

ZADANIE 19

Oblicz następujące wyrażenie

J Q2 + 2 log?

Rozwiązanie:

Najpierw skorzystaj z własności potęg, czyli ze wzoru

ar* = ar ar

Teraz skorzystaj z własności dotyczącej togarytmów a*** = p.

102*2 log7 _ 10“ * 1 0“ 1°®? ⁼

= 100-10^,OJt7 = 100* 10^ll*⁴⁹ = = 100-49= 4900

ZADANIE 20

Dla jakich wartości parametru m równanie: 4’ - 3 • 2^X - m = 0 ma dwa różne pierwiastki?

Rozwiązanie:

4’ - 3 • 2^X ~ m = 0 Niech 2* = /, / > 0 I² - 3/ - //; = 0

Aby rozwiązać to równanie wykładnicze, musisz wprowadzić zmienną pomocniczą za 2* f i w ten sposób otrzymasz równanie kwadrato we zmiennej f.

A > 0

/,f₂>0

w, + /,>o

Równanie kwadratowe ma dwa różne pierwiastki wtedy gdy, A > 0.

Prócz tego warunku pamiętaj, że wyjściowe równanie jest równaniem wykładniczym, więc zgod nie z def. funkcji svykładniczej jej podstawa musi być dodatnia. Aby istniały dwa różne pierwiastki tego równania f, i f, muszą być oba dodatnie. Na podstawie wzorów Viete'a oba pierwiastki równania kwadratowego są dodatnie, gdy spełniają warunki x, + x_ł>0ix_|-^>0

A = 9 - 4 • 1 • (-/;/) = 9 + 4/// 9 + 4/;; > 0 4/n > -9 / :4 9

^,U 4    9

czyli e ", +oc j

ni

-m> 0 / : (-1) ni < 0, czyli m g (-co, 0)

f, + /j = 7 = 3^>0

W ten sposób obliczyliśmy rozwiązanie warunku A > 0

Przypomnijmy sobie wzory Viete'a dla równania kwadratowego w postaci ogólnej ał + bx + c = 0. a r 0

zatem m g R

87