04 maj 12

TKORIA SPRĘŻYSTOŚCI 1 PLASTYCZNOŚCI

EGZAMIN NR 1, ROK AKAD. 2011/2012 • 30.05. 20l2r. • KMIliM WILiŚ PG

Czas trwania egzaminu: 105 minut (1 godz. 45 min.)

V»'iULiL

•    Każde z zadań części zadaniowej należy rozwiązać na osobnej kartce (kartkach), natomiast wszystkie zadania części teoretycznej należy rozwiązać na jednej kartce'

•    Wszystkie kartki należy podpisać (imię. nazw isko, numer indeksu, grupa, numer sali w której odbywa .się egzamin)!

•    W przypadku braku rozwupania zadania (zadań) także należy oddać podpisom/ kartkę (kartki) >

CZĘŚĆ ZADANIOWA

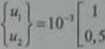
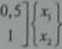
ZADANIE 1: Deformacja w PSN określona jest następującym wektorem przemieszczeń

•) Obliczyć przemieszczenia punktów: /l(0;0). £(l;0), C(l;l), Z>(0;1) oraz £(0,75;0.75).

b)    Naszkicować deformację rozpatrywanego PSN.

c)    Obliczyć składowe tensora małych odkształceń w punkcie £(0,75;0,75)

d)    Obliczyć składowe tensora naprężeń Cauchy w punkcie £(0,75;0.75).

c) Wykazać, że w każdym punkcie tego układu, przy zerowych siłach masowych, spełnione są równania równowagi. Dane: £ = 10‘A£«; i'-0,25.

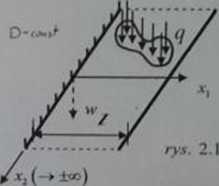
ZADANIE 2: Napisać funkcję ugięcia nieskończonego pasma płytowego o szerokości / = 6m, lewostronnie utwierdzonego, o prawostronnej krawędzi swobodnej (rys. 2.1), pod działaniem obciążenia równomiernie rozłożonego q - 90kPa-cotisl, działającego na całej powierzchni pasma.

Naszkicować przekrój powierzchni ugięcia płaszczyzną x₇ =0 .

Napisać funkcje i narysować wykresy momentów płytowych:

A/,, dla x, =0 oraz M_u dla x_i =0,5■/

Uwaga: W przypadku pasma płytowego warunek zerowej zastępczej siły poprzecznej ma postać: w_ł|lt = 0

ZADANIE 3: Obliczyć zapas bezpieczeństwa, osobno wg hipotez Treski i H-M-H, przyjmując równomierny wzrost wszystkich składowych tensora naprężeń.

a

12	0	-12
0	—4	0
-12	0	30

[MPa\,

<7_# s.50[MPa]

• Określić, w ogólny sposób, kryteria obszaru bezpiecznego wg hipotez Treski i H-M-H.

__CZEŚĆ TEOKETYCZNA

Vwara: W nrsynadku udzielenia odpowiedzi świadcząca a niezrozumieniu zagadnienia. zadgnjs_mQlć ZOśtać ocenione na 0 nkt'

PYTANIE 1: Przeprowadzić bilans równań i niewiadomych ogólnego zadania teorii sprężystości (podoć ogólną formę równań - wskaźnikową lub absolutną), a następnie objaśnić występujące w wyżej wymienianych równaniach symbole wielkości tensorowych, podając ich rząd (walcncję),

Czy w bilansie tym występują równania równowagi oraz równania zgodności (mcrozdzielności) odkształceń?

PYTANIE 2: Wyjaśnić następujące pojęcia: sprężystość, wielkość tensorowa Walencji II oraz jej niezmienniki, płaszczyzna dewiatorowa.

PYTANIE 3: Opisać metodę rozwiązywania zagadnień płaskich (PSN. PSO) z wykorzystaniem funkcji Airy. podać korzyści tej metody

Wyrazić w obu przypadkach składowe stanu naprężenia względem tunkcji Auy.

PYTANIE 4: Narysować występujące w cienkiej płycie sprężystej, w układzie kartezjańskim. siły wewnętrzne: momenty i siły poprzeczne płytowe; wykonać odpowiednią ilustrację dotyczącą tychże sił wewnętrznych.

W jakim celu wprowadza się zastępczą siłę poprzeczną na brzegu płyty?

PYTANIE 5: Podać uogólnione prawo llooke’a. opisać (zinterpretować) występujące w nich stałe materiałowo (£    ).

podać interpretację równań w stanic dwuwymiarowym (2-D).

PYTANIE 6: W jakim celu formułuje się hipotezy wytrzymałościowe (warunki plastyczności)?

Dlaczego hipotezy: freski i H-M-H lepiej opisują zachowanie się materiałów, niż hipoteza Galileusza.

I l.ńfWi.M Slownnek. V KonopimU K. WmUlnunn . I_t»u i^tnileta ./Uaiftcm.w. 1    iu l.rok *1*1 2011/2012 . KMBlM WlU$|«r,