lz54

TEORIA SPRĘŻYSTOŚCI ■ Pl_fASTVCZNO$fl EGZAMIN NR 2, ROK AKAD. 2011/2012 • 11.09.2012r. • KMBIMWIUSF Cmi trwaniu cgwminu: 105 minut (1 godz. 45 min.)

“toJr i ** Wici »di*te*i mktf tK*ą* * Urtct lUrtbtk **<**! attfldu iMl

•    IłcyiiWlxfOimirt)podpisało-if.mutommrlMkim fnęatmirmk^k^t^roaśftpmoł

•    Wprąpotol ¹    |".....^n^^ndtHnmmirntmkrtkłńmśUt

CZĘŚĆ ZADANIOWA

J*,?:2i_rji -I0>| ■•lA'V⁷*.

i) Wyznaczy* ttnior mutycli odkształceń r -*0.5(V'm4 V«') (lub równoważnie /,    , *!<„)),

oraztensornaprężeń ą-kUtnlpr(lubrównoważnie: o_%okdf_m*lps_t\, b) Sprawdzić, czy przy 0,«l$MPa dam stan naprężenia jol bezpieczny. itosowmc do lnpoic/> H M-H HipotezaH-M-H: (er,,-?,/*[o_a-ęj♦(<v<r„)^>*6 (er,/4^*♦ <r_lł^,)«2 O,¹.    1

■ii mmMśi

ZADANIE 1: Deformacji w I* okrtśkmi jest wektorem pr/cmies/.aciV,ą a«

Dane: £»2O0GPtf; »• -0,3. Miife Unie: /.=

(Uv)(l-2f)" 2*(l*v)

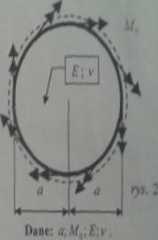
ZADANIE 2: Dana Jest płyta kołowa, swobodnie podpina, obciążona na brzegu ciągłym momentem zginającym Af₀ (ry», 2.1).

Zimna jest całka ogólna równania płyty H(f)«.4r^;lnr.CtoMA.

Wypisać warunki prowadzące do wyznaczenia stałych: Ą\ B.C, A'

Przyjmując, ze z warunków tych wynika m in redukcja wyrazów logarytmicznych, poda* wartości tych stałych.

Poda* Arnkcję powierzchni ugięcia, funkcje momentów radialnych i obwodowych względem współrzędnej r onz naszkicować wykręty tychże wielkości wzdłuż średnicy.

^Wz®^r*(Pny aymetrtl obrotowej): A/_W(r)»-D.(w._w4r*^,-v*w.,) oraz A/^(r)--|>.(r ‘

ZADANIE 3: Obliczyć zapas bezpieczeństwa, osobno wg hipotez Troki i H-M-H, w stosunku do podanego niżej SN:

\o_n =o., ■*- =<r_n ■ lOAlPo

. ' . _l/n; o^mPa.

I powstałe składowi = OMPa

Prcyją* równomierny wzrost wszystkich składowych wyjściowego stanu naprężeń

O-    CZEŚĆ TEORETYCZNA

PYTANIE 1: Wyjaśnić następujące pojęcia: tensor sprężystości, warunek uplastycznienia (hipoteza wytrzymałościowi), energia właściwa odkształcenia postaciowego.

PYTANIE 2: Poda* warunki brzegowe krawędzi AB. GD i DA płyty, zilustrowanej na rys.4.1.

'    .    .7 lllllium

10 $ 10 5 10 5 10 1 I0|_

Obliczyć składowe wektora naprężenia w przekroju o normalnej, będącej dwusieczną kąta prostego między osiami płaszczyzny Or,x,.

PYTANIE 4: Na czym polega tensorowy charakter naprężenia?

Sk^d wynika symetria tensorów: małych odkształceń i naprężeń?

PYTANIE 3: Dany jest tensor naprężenia: _ffa

krawfdł

swobodna I *

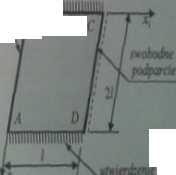
ryi.4.1.

* A.    'i ■

PYTANIE 5: Podać uogólnione prawo Hookc'a (poda* zależności między naprężeniami, a oAunkfu—i). opM* (zinterpretować) występujące w nich stale materiałowe (£; v), poda* interpretację równań w sunie dwuwymiarowym.

PYTANIE 6: Wjukim celo foimutajeaę hipoteąr

Dlaczego hipolcy: Treski    lepiej opiająz«hoft'anieatiBM°^ialH«^''^|P^||ltaG*^llltllg|g __