06 czerwiec 13

TEORIA SPIU;/VSTO$t-| I H ASryC/lNOŚCI EGZAMIN NR 1 • ROK AKAD. 2012/2013 • 24.06. 20lir. • KMRIM WILiŚ PG

Cza* trwania egzaminu: 120 minut (2 god/.ł

lliUŁti

•    K>iide - zadań części zadaniowe) należy rozwiązać na osobnej karne (kartkach), ruitomiait wszystkie ntdoma części teoretycznej należy rozwiązać na jedne) kartce'

•    )V.<czyxtkic konta należy podpisać (imię, nazwisko, numer indeksu, grupa oraz numer mli, w ktiiirj odbywa '<r egzamin)!

•    Wpnypadbi braku mzwupanio zadania (zadań) Uikte milrZr <hMi. podpttaną kartkę /kartki)¹

I    CZEŚĆ ZADANIOWA

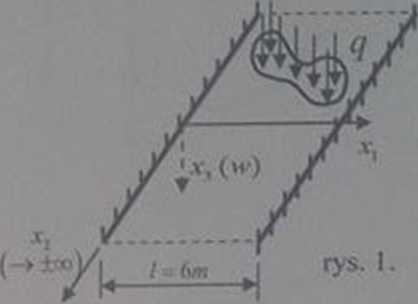
ZADANIE I: Nieskończone pasmo płytowe o szerokości / 6m, obustronnie utwierdzane (wg rys. 1.). olici;|*onc jest w sposób ciągły i równomicmy q lOkPa =comi.

A) Napisać funkcje i narysować wykresy tr(x, 0). W_l((*. 0),A/„(t, 0..«, 1/2).

0) Obliczyć dla podanego pasma płytowego ekstremalne naprężenia: a,, ora/ a_v oraz naprężenia zredukowane według hipotezy I I M 11 (rr, , __MUTł).

G) Podać dopuszczalną wartość obciążenia pasma </ |kPa|. jeżeli naprężenia graniczne wynoszą: R„ = 150MPa .

Dunc: E - l00C»Pa; v - 0.2 oraz h = 5cm (grubość pasma).

ZADANIE 2: W ośrodku ciągłym dany jest wektor przemieszczeń: u u,

10.r, 161. 8.v, i 10 x,

-9x,

lO^m]

A)    Wyznaczyć tensor małych odkształceń r - 0,5(V« i V</ ) (lub równoważnie:    0.5(», • «, )).

B)    Wyznaczyć tensor naprężeń Ca uchy ą A I trn e 2 fi /. (lub równoważnie: o A «V i;_u e- 2// r: ).

C ) Określić, niezależnie według hipotez Treski i H-M H. czy dany stan naprężenia jest bezpieczny.

Cir,inicznc naprężeniu w stanic jednoosiowym wynoszą: ir₍, JjWMflPa. SCO

»s    p

Dane: E 200<iPa . v = 0,25 . stale Larnc: A -> —-7.;—- --; // ^c ₍,    . •

(I *i')(l -2r)    2(1 * r)

Z.ADANIE 3: I.iiczjj pierścieniowa o grubości g = 2ern ściskana jest '/obu Mion wewnęiizncj 1 z.cwnęir/ncj, /> -■ lOMPa -Dane: Promień wewnętrzny tarczy wynosi n 2m. natomiast promień zewnętrzny b 4m. F. » 100(iPa; i* = 0,25 ^p —

A)    Podać analitycznie i graficznie rozkład naprężeń radialnych 1 obwodowych w tarczy Na wykresach zwrócić uwagę na wypiikłośćwklę-lośt prc/cntowu.nych funkcji.

Wykitztłwka: W ogólnym przy padku obrotowej symetrii w PSN lub PŚ6, w danej odległości 1 od środka układu, zachodzi:

er -~-r2C om/ o    —4- + 2C. udzie: I. C slttłc

/    r'

B)    Obliczyć na obu krawędziach tarczy wcwnęlr/nci 1 zewnętrznej naprężenia główne er,, oiaz zmianę grubości tarczy A# .

C)    Podać wartość obciążenia pasma />|MPa|. przy którym /ostanie osiągnięty stan graniczny według hipotezy IIM H. jeżeli naprężeniu graniczne wynoszą: a„ lOOMPn

CZEŚĆ TEORETYCZNA

Lwosu: H tmpodku u,bieleniu    iatn2v«io^iiizsjj/jucdi!iJi'"io)tHMh:astiJisnuLJistkaU

PYTANIE 1: Naszkicować przebieg naprężeń normalnych tr_n w przekrojach A A i B B okresowo podpartego i obciążonego pasma tarczowego. zilustrowanego rn» rys 2

l*Y I ANIE 2: Dany jest stan naprężenia w punkcie O o„

\ 10 2 0 2 -3

5 3    0    £

Obliczyć wektor naprężenia w punkcie O, w przekroju danym równaniem płaszczyzny ix * 2y + 6r - 0.

PYTANIE 3: Wyjaśnić różnicę między pojęciami związki konstytutywne, a llniowosprężystc prawo Hooke'*    ^v ^

Zinterpretować stale materiałowe l. ora/. i*. Potłuc graniczne wartości liczby 1. opiMis każdy z granicznych przypadków

PV TANIE 4: Przeprowadzać bilans równań 1 niewiadomych ogólnego zadania teorii sprężystości. Dlaczego problem ten jcsi statycznie niowy7.11.u żalny? laką rolę w w w bilansie odgrywają równania nicto/d/iclnosci (zgodności odkształceni?

1

OtsisJti. M SVmr«v«.*i V    A» K Wirtkrinwmi M <Wi«jbt»i• /<v«w A- ■ >>.    >'•. I . j itr I. sok iwt WlJtolP •'KńtłltM wh •- ;•>.