01 czerwiec(2) 11

TEORIA SPRĘŻYSTOŚCI I PLASTYCZNOŚCI

EGZAMIN NR 1, ROK AKAD. 2010/2011 • 16.06.2011r. • KMBiM WILiŚ PC

Czas trwania egzaminu: 105 minut (1 godz. 45 min.)

Uwagi:

•    Każde z zadań części zadaniowej należy rozwiązać na osobnej kartce (kartkach), natomiast wszystkie zadania części teoretycznej należy rozwiązać na jednej kartce!

•    Wszystkie kartki należy podpisać (imię, nazwisko, numer indeksu, grupa, numer sali w której odbywa się egzamin)!

•    W przypadku braku rozwiązania zadania (zadań) także należy oddać podpisaną kartkę (kartki)!

CZĘSC ZADANIOWA

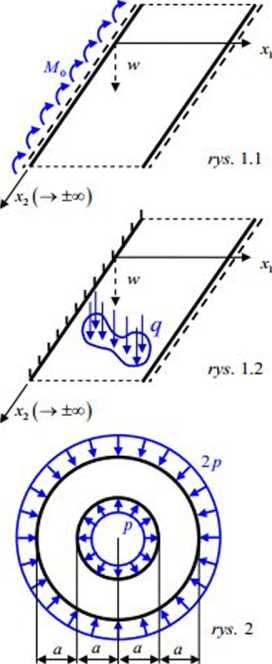
ZADANIE 1: Funkcja ugięcia swobodnie podpartego pasma płytowego o jednostkowej szerokości, pod obciążeniem równomiernym q

ma postać: u* = -^(.t⁴ - 2*? + -V,)

W przypadku obciążenia momentem A/₀ rozłożonym na lewej krawędzi (rys 1.1) funkcja ugięcia powyższego pasma płytowego

ma postać: u ^l,° =    ~ ^^xi ⁺ ^^x\)

Wyznaczyć funkcję ugięcia pasma płytowego lewostronnie utwierdzonego, prawostronnie swobodnie podpartego (rys. 1.2) pod obciążeniem równomiernie rozłożonym q.

ZADANIE 2: Wyznaczyć naprężenia główne (T_(l) na obu brzegach:

wewnętrznymi i zewnętrznym nieskończenie długiej rury grubościennej (rys. 2). Oba brzegi są obciążone równomiernie. Dane: p,    V.

Wskazówka: W ogólnym przypadku obrotowej symetrii w PSN lub PSO, w danej odległości r od środka układu, zachodzi:

A    A

<T_ = —r + 2C oraz <7 = —- + 2C, gdzie: A, C - stałe

ⁿ f.2    w>    _r2    °

ZADANIE 3: Obliczyć zapas bezpieczeństwa, osobno wg hipotez: Treski i H-M-H, przy <7_o=30j\fPa, zakładając przyrost jedynie składowej <7₃₃.

15	6
6	6
0	0

0

0

-9

[MPa]

_CZĘSC TEORETYCZNA_

PYTANIE 1: Jakie uproszczenie w analizie tarcz w biegunowym układzie współrzędnych przynosi założenie obrotowej symetrii? Jakie wielkości opisują całkowicie w tym przypadku stan naprężenia w danym punkcie?

PYTANIE 2: Podać ogólne określenie wielkości tensorowych. Podać przykłady wielkości tensorowych: skalarnych, wektorowych oraz Walencji II. występujących w Teorii Sprężystości.

5*"£Tj |    r7*"£T|₃ ^ C~ £ [i

dx₂dx₃    dx_{dx₂ dx_xdx₃    dx_x

PYTANIE 3: Wykazać słuszność następującego równ. nierozdzielności:

PYTANIE 4: Wyjaśnić dlaczego w hipotezie Treski mamy r₀ = 0,5 • <7₀,

gdzie: r₀, <T₀ - odpowiednio: graniczne naprężenia styczne i graniczne naprężenia normalne

J. Górski. M. Skowronek. M. Gołota. K. Winkcbnonn • Teoria*prf^;xtaxa iplaini-zności — t.g/amin nr I. rok akad. 20I(V2011 • KMBiM WILiŚ PG