061

+(

ds . ₂ .

v=-=\r-2, dt ²

jatem

	m	' 1
	_^	i

I¹ / j

120    VI. Pochodne funkcji postaci y=f(_x)

Wyprowadzenie ogólnych wzorów na pochodną dowolnego rzędu danej funkcji na ogół zagadnieniem trudnym. Jeżeli funkcja ma postać lub daje się przedstawić w postąp iloczynu dwóch prostszych funkcji, dla których można znaleźć łatwo ogólne wzory ^ pochodną rzędu n, to pochodną rzędu n danej funkcji wyznaczamy ze wzoru Leibnj^ Niech będą dane funkcje u=f(x) i v=g(x) mające pochodne aż do rzędu n włą_CZll;_ę Wówczas funkcja y=uv ma pochodną rzędu n wyrażającą się wzorem

(6.2.3)    /*>=u⁽"⁾t>+Qu^l“"¹V+Q“^<""²⁾«''+...+Qu⁽"^_łV*⁾+...+«t)⁽">.

Jest to wspomniany wzór Leibniza-, występujący we wzorze tym symbol Newtona został określony w § 1.9.

Zadanie 6.220. Obliczyć czwartą pochodną funkcji y=x⁵ cos x.

Rozwiązanie. Niech u=x^s, u=cos x. Stosując wzór Leibniza dla n=4 otrzymujemy y<⁴W⁴⁾i;+4u"V+6u"v" +4uV" +uv^w.

Należy tu podstawić;

u=x⁵,    u' = 5x⁴,    u"=20x³,    u"'=60x², u⁽⁴⁾=120x,

v=cosx, v' = — sinx, v" = — cosx, t/"=sinx, u⁽⁴⁾=cos x. Otrzymujemy wówczas

y⁽⁴⁾=120x cos x - 240x² sin x - 120x³ cos x +20x⁴ sin x +x⁵ cos x.

Zadanie 6.221. Znaleźć pochodną rzędu n funkcji y=e~^x sin x.

Rozwiązanie. Niech u=e~^x, D=sinx. Wówczas

u'= — e~^x, u"=e~^x,    u'"—-e~^x, u^w=e~^x,

i ogólnie

u⁽ⁿ⁾=(—l)"e^-*.

Prócz tego wiemy (zad. 6.219), że pochodna rzędu n funkcji o=sin x wyraża się wzorem v^<n) = sin (x+n ■ ^Tt). Stosując wzór Leibniza otrzymujemy

y^M=(-1)" e^_x sin x +(-1)*"¹ ne~^x sin (x +in) +

+(-l)""²-in(n-l)e“^xsin (x+2- %iz)+...+

e ^Xsin(x+/c^-57t) + ...—

— ne^_xsin (x+(n — 1) •    +e~^x sin(x -t-n • |ti) .

Oczywiście, po prawej stronie można wyłączyć przed nawias e~^x.

Zadanie 6.222. Dane jest równanie s=\t²—2t ruchu prostoliniowego. Wyznać moment t, w którym prędkość ruchu będzie równa zeru. Znaleźć przyśpieszenie rił®**

Rozwiązanie. Prędkość

)=0, gdy 1=2, & przyśpieszenie

d²s

⁼~d?⁼

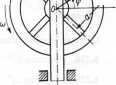
Zadanie 6.223. Korba k umieszczona na obwodzie obracającego się koła c wprowadza _ff ruch suwadło s (rys. 6.10). Prędkość kątowa koła jest stała i wynosi co, odległość korby od osi obrotu jest równa a. Wyznaczyć prędkość i przyśpieszenie suwadła w danym momencie czasu t.

Rozwiązanie. Suwadło porusza się ruchem harmonicznym o amplitudzie a i pulsacji co:

/=asin <p=asiaojt.

Prędkość chwilowa suwadła: dl

—=aco cos cot, dt

a przyśpieszenie chwilowe suwadła: d²l ₂ .

—2= -aoi smcot.    Rys. 6.10

Zadanie 6.224. Droga przebyta przez ciało przy swobodnym spadku, z uwzględnieniem oporu powietrza, wyraża się wzorem

vj. .gt s=— ln cosh —, g

^8dz,e °1 ^yfgla, g jest przyśpieszenie ziemskie, a - współczynnik uwzględniający opór Powietrza. Wyznaczyć przyśpieszenie ruchu spadającego ciała w zależności od czasu t. Rozwiązanie. Mamy

ds    gt d²s    1

— = o₁tgh—, —y~g--

dt    oj dt²    ₂gf

cosh —

^vi

°^dy wówczas    —►(), a więc po dostatecznie długim czasie ruch odbywa się prak-

^yc2nie bez przyśpieszenia, czyli jest ruchem jednostajnym z prędkością u,.

Zadanie 6.225. Wyznaczyć dla chwili t=j^n s wartość siły, pod wpływem której ^{0 0} masie m = 10 g porusza się ruchem określonym przez równanie y=3 sin³ 5r (w cm).