087(1)

VIII. Na podstawie otrzymanych wyników badania funkcji sporządzamy jej wykres (rys. 76).

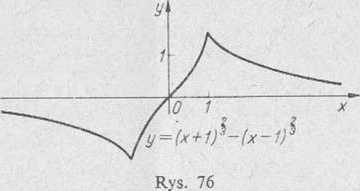
4) I, II. Funkcja y = sin⁴x -(- cos⁴x jest określona i ciągła na całej osi liczbowej.

III.    Jest to funkcja parzysta, ponieważ zachodzi y(—x) = y(x), a prócz tego okresowa, gdyż y(x) - y |x+™J. Okres jej wynosi n/2. Wystarczy więc zbadać zachowanie się funkcji oraz sporządzić jej wykres w przedziale [0,-J); w pozostałych punktach osi liczbowej i przebieg funkcji, i jej wykres będą się powtarzały.

IV.    Gdy x = 0, y — 1, czyli y # 0. Wykres przecina oś Oy w punkcie (0, 1) i nie przecina osi Ox. Funkcja ma wartość dodatnią dla każdej wartości x.

V.    a) Ponieważ funkcja jest ciągła na całej osi liczbowej wykres jej nie ma asymptot pionowych.

b) Mamy

k —

lim Z-

x-*+co

— lim

sin⁴x )-cos⁴x x

--- 0

oraz

b = lim (y—kx) = lim (sin⁴x-| cos⁴x)

X-*+.<Q

czyli b nie istnieje. To samo zachodzi, gdy x -* —co. Zatem wykres funkcji nie ma w ogóle asymptot.

VI. Pochodna funkcji

y = 4sin³xcosx—4cos³xsinx = 4sinxcosx(sin²x—cos²x) =

= — 2sin2xcos2x = —sin4x

i w przedziale j^O, Ą J jest równa zeru w punktach x — 0, x = jr/4.

Są to punkty krytyczne. Ponieważ y wszędzie istnieje, innych punktów krytycznych w przedziale tym nie ma. Badamy punkty krytyczne-, wyznaczając w nich znak y" (wg reguły Ilb). Mamy y" = —4cos4x, skąd y"(0) = — 4 < 0, czyli x = 0 jest punktem maksimum, przy czym y_max =

— y(0) = 1. Dalej /'    = 4 > 0, a więc x = ~ jest punktem minimum,

przy czym y_min = y (-j) = ~.

W przedziale (o, -jj- j pochodna y' < 0 — funkcja maleje, a w przedziale

(t* t) P^oc^^ocł-^na y > 0 — funkcja rośnie.

VII. Druga pochodna y" = —4 cos 4x istnieje wszędzie i w przedziale [O, y j jest równa zeru dla x = y i x — -^~. Punkty te mogą więc być odciętymi punktów przegięcia. Badając znak y" w ich otoczeniu stwier

X	0	71 Y	71 7	3n T~	n T
y"	-	•	+	0	-
y	wyp.	pkt przeg.	wid.	pkt przeg.	wyp.

dzamy, że w przedziale jo, wykres funkcji ma dwa punkty przegięcia

U 3\ . (3n_ 3\

V8 ’ 4/ ¹ l 8 ’ 4/’

Rzędne tych punktów zostały obliczone ze wzoru na y.

W przedziałach [^0, yj i ^y-, y), w których y” < 0, wykres funkcji

jest wypukły, a w przedziale ^    ^ ] , w którym y" > 0, wykres ten jest

wklęsły.

12 Metody rozwiązywania zadań 177