101716672313076467966h08561661149324736 n
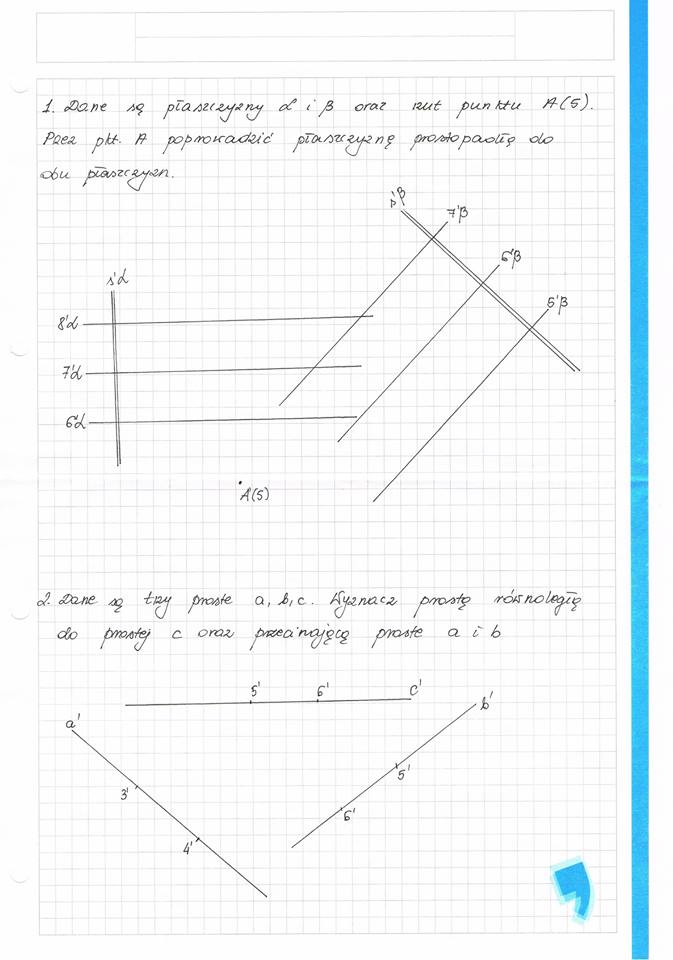
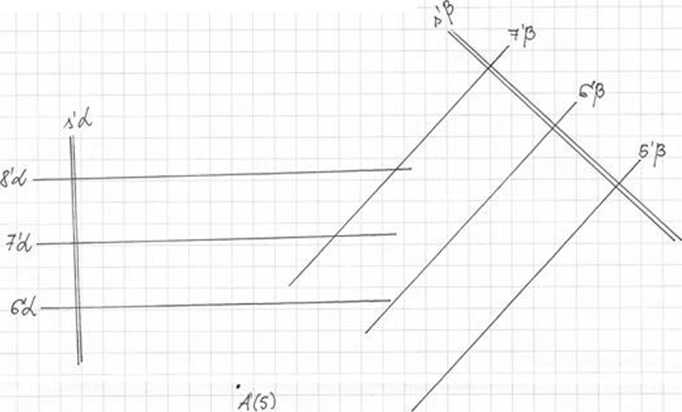
/ <Z&r>t a<$ pZaAZ(&jJnj oć e fi oraz tzcnf pu.n kt-u &£$).
Pcez pi/-, ft pop/rotccoete/ć pTo*./yuzy-znp pro/bk?pccolT? oto <cóu puv>zcpj*zn.
o?. <Z*uie /ą -kpAj proste. o,J>,c. fija/uzc* prrcrrfp 'rcMnol&pę cfo proA-fep a o rai; p^anpjpcp pyy&tfó. cl Z 6
1
Wyszukiwarka
Podobne podstrony:
img128 c średnie wart. r> flr Poprawki cT Azymuty oc *> I> I fi - i raf r <T-
img344 Parametrami rozkładu są teraz: wektor średnich fi oraz macierz kowariancji Z. Macierz ta zale
P1150611 I 3 CD6 Ś 10cm 7-5 tcm Z-6 . _r A9 fi) oraz ceramik® 2-8 Dcm R1f 3. U. Br
L Artemise 1 URiglt tT^sctiOM* vcŁl ic<iCea ćefniOi^lćtufe* Oc^fi^col^uĄCM/OolioW 0«>
Eidos lUMJ,.,...---- M IX 1 1 Ul 1 1 I! J PU »M l« •». •• fłl«» »•’ »• • U r • iu fi »?
granice3 (i*N >~?0 —5V^^X" oC T -fi W) — U X2- ] *
kioliwłtn- Hotf Wol t Chwila II* S 1.i.m> peom fi*uK auh pu*iwy/cg<» uwi<v.loni»i
V Rys. 26 yęfezZ! w, = -a>0 clgat 0,0 H 2R „ c(ga = —= — = — = 2, OC fi fi co, =(>
DSC07362 142Geometria analityczna w przestrzeni dla pewnego UR{0}. Mamy fi = (1,1,1) oraz SP= (-z, 1
ODPOWIEDZI Macierze i geometria 2 204 Rozdział 1. Układy równań liniowychRozdział 4 (str. 115) 4.1
P1150611 I 3 CD6 Ś 10cm 7-5 tcm Z-6 . _r A9 fi) oraz ceramik® 2-8 Dcm R1f 3. U. Br
14 Liczby rzeczywiste Dowód przeprowadzimy przez sprowadzenie do niedorzeczności. Niech np. oc>fi
więcej podobnych podstron