163(1)

W całce iterowanej Ix funkcja F(a, fi) jest najpierw całkowana względem fi, przy tym oc traktuje się jako stałą, a następnie otrzymany wynik całkuje się względem cc.
W całce iterowanej /2 całkowanie przebiega w odwrotnej kolejności, najpierw całkujemy względem cc, traktując przy tym fi jako stałą, a następnie otrzymany wynik całkujemy względem fi.
Z reguły przy pierwszym całkowaniu granice są zmienne i zależą od tej zmiennej, która jest przy tym traktowana jako stała. Natomiast granice przy drugim całkowaniu są zawsze stale.
Jeżeli obszar całkowania D jest odniesiony do układu współrzędnych prostokątnych xOy i jeśli jego podział na obszary częściowe jest dokonany przez siatkę prostych równoległych do osi układu (rys. 151), to pole obszaru
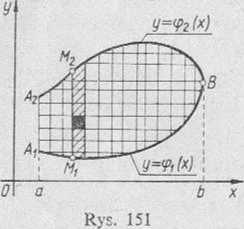
częściowego jest równe ds = dxdy (jako pole prostokąta o bokach dx i dy) i J / f(M)dS = /J /(.v, y)dx dy
D ~D
Jeśli przy tym obszar D ma tę własność, iż każda prosta przechodząca przez wewnętrzne jego punkty i równoległa od osi Oy przecina granice obszaru w dwóch tylko punktach (rys. 151), to obszar ten można przedstawić za pomocą następujących nierówności
<Pi(x) <y aśżx^b
gdzie: y = cpi(x) i y = <p2(x) są odpowiednio równaniami dolnej i górnej (A2M2B) linii granicznej, zaś a i b są odciętymi skrajnego lewego i skrajnego prawego punktu obszaru D. W tym przypadku całka podwójna wyraża się całką iterowaną o postaci
b
J f f(x,y)dxdy = J dx jf(x,y)dy (1)
D a <r,(x)
We wzorze tym całkować należy najpierw względem y, w. granicach od >'i — <Pi(x) do y2 = T2M ograniczających zmienność y przy stałej, ale dowolnej wartości x, a następnie — względem x, w granicach od y, = a jo ,v2 = b, które to wartości są krańcowymi wartościami x (najmniejszą i największą) w całym rozważanym obszarze D.
Jeżeli okaże się przy tym, że dolna lub górna linia graniczna składa się z kilku części, opisanych różnymi równaniami, to obszar D należy podzielić za pomocą prostych równoległych do osi Oy na części, tak aby w każdej z nich linia graniczna dolna i górna były opisane każda'jednym równaniem.
y
c
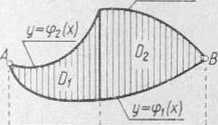
Rys. 152
Wa
b x
c
0
x
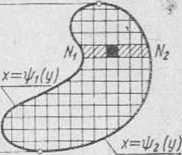
Rys. 153
Na przykład obliczanie całki podwójnej po obszarze D, przedstawionym na rys. 152, sprowadza się do obliczania dwóch całek iterowanych
I I udxdy — f I udxdy + | J udxdy
D
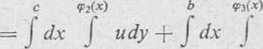
udy
a
TiC-O
c
?l(*>
Jeżeli natomiast proste równoległe do osi odciętych Ox i przechodzące przez punkty wewnętrzne obszaru D przecinają jego linię graniczną tylko w dw óch punktach (rys. 153), to obszar można określić nierównościami o postaci
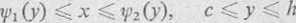
gdzie: x = ip1(y) i x = y>2(y) są odpowiednio równaniami lewej (CNJI) i prawej (CN2H) linii granicznej, a c i h są rzędnymi skrajnych (dolnego i górnego) punktów' obszaru D.
329
Wyszukiwarka
Podobne podstrony:
DSC00072 (6) Funkcjonalny podział glebowej materii organicznej • Materię organiczną (MO) gleb traktu
1.1. Czym jest sztuczna inteligencja? Istnieją też definicje bardziej praktyczne, traktujące Al jako
Skupienie uwagi Jest to wyższy stopień koncentracji. Na tym szczeblu skupia się myśli w
Współczynnik długości wyboc/eniowej słupa f.ix — /u(Ci,Ca) jest funkcją sztywności jego zamocowania
W całce iterowanej /j całkowanie odbywa się w odwrotnej kolejności, najpierw całkujemy względem &
Image1932 1 1 lim xsin— = O gdyż lim x = O i funkcja sin— jest ograniczona, bo x-»0
Image1940 Funkcja f(x) = y = — ,x^0 , y X O dlax = 0 jest ciągła w Xg = O, bo lim f(x)= lim e/x = 2
Image318 Funkcje arytmetyczne i logiczne realizowane przez układ 181 przy założeniu, ie sygnałem akt
Zdjęcie1205 5. DYSTRYBLANTA I HISTOGRAM ZMIENNEJ LOSOWEJ SKOKOWEJ Funkcja F(x) * P (x <x) nazywan
Zdj?cie0453 Gęstością rozkładu zmiennej losowej: >4. Jest funkcja (tu), (b) i (c); C. są wszystki
Jako jest najpierwszą powinnością urzędu mego, czułość ku konserwacji Oby watelów pod bokiem J. K. M
więcej podobnych podstron