188(1)

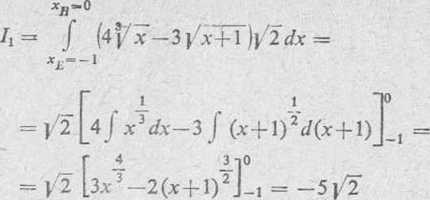
2) Daną całkę przekształcamy na całkę oznaczoną względem /. Mamy: = cos³/, dx = — ?cos²/sin tdt;y — sin³/, dy = 3sin²/cos tdt; dl —

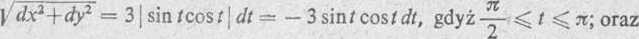
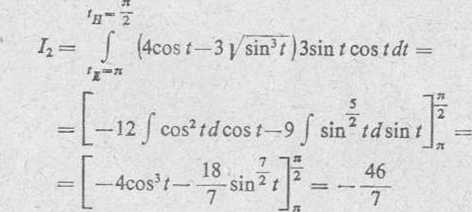
874. Dane są punkty A(3, —6, 0) i B(—2, 4, 5). Obliczyć całkę krzywoliniową I — j xy¹dx+yz¹dy—zx²dz, gdy krzywą^iłkowania C jest: 1) odcinek prostoliniowy OB, 2) łuk okręgu AB, dany równaniami x¹'-\-y^ijr +z² = 45, 2x+y — 0.

Rozwiązanie: I) Najpierw piszemy równanie linii całkowania, czyli prostej OB. Z ogólnego wzoru na prostą przechodzącą przez dwa punkty

*—*i ₌ y-y i ₌ z~z i

y2 y i    z₂—Zi

otrzymujemy —-j =    = • -.

Przyrównując te trzy równe sobie stosunki do parametru /, nadajemy kanonicznym równaniom prostej OB postać parametryczną x — —21, y — 41, z = 51.

Z kolei, na podstawie tych ostatnich równań, przekształcamy całkę krzywoliniową na zwykłą całkę o zmiennej całkowania / i obliczamy ją. Mamy

t_t=-\

f -2t(4t)²(-2dt)+4/(5t)²4dt-5t(-20^z5dt =

'•“O ,

- 364 f t'dt = 91 o'

2) Dane równania okręgu sprowadzamy do postaci parametrycznej. Podstawiając x — t, z drugiego równania otrzymamy y = —21, a z pierwszego z = y'45 —5r , skąd dLv == dt, dy = —2dt, dz —--* ^oraz

7₂ =    |    / (—2/)²c/f-h (—2r) (45—5r²) (—2dt)—

- ylTZiff    - / (180/-17,>)* = -173-J

875. Obliczyć całki krzywoliniowe:

1) f 2.rdi-(j;4 2y)d> i 2) f >’cos.Yrfx-)-sin.vd^ry

-t    ■+/

po obwodzie trójkąta o wierzchołkach A(— 1, 0), B(0, 2) i C(2, 0).

Rozwiązanie: 1) Tym razem zamknięta linia całkowania (rys. 192) składa się z trzech odcinków, leżących na różnych prostych (danych różnymi równaniami). W związku z tym całkę krzywoliniową po łamanej ABC A obliczamy jako sumę całek, wziętych wzdłuż odcinków AB, BC i CA.

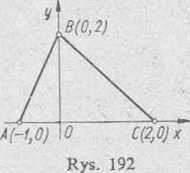
Pisząc równanie prostej AB, mające postać y—2x = 2, i biorąc je za punkt wyjścia, przekształcamy całkę krzywoliniową po tym odcinku na •zwykłą całkę ze zmienną .v. Mamy

x_B °

y = 2x-\ 2, dy = 2dx, f = —8 J (a:+1)c/.y =

AB    x_A =. -1

= -4[(.y+1)²1°-i = -4

379