197(1)

Przekształcając całkę powierzchniową po lewej (wewnętrznej) stronie trójkąta ABC na całkę podwójną i obliczając ją, otrzymamy

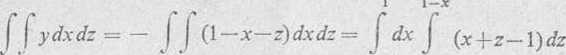
ABC

ACO    6    0

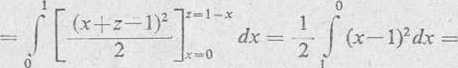
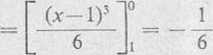
Całka

I I ydxdz — I J ydxdz = 0

BCO

ABO

ponieważ płaszczyzny BCO i ABO są prostopadłe do płaszczyzny xOz (por. str. 390). Z kolei całka

I I ydxdz = I | 0dxdz = 0

Zatem K = —

908. Posługując się wzorem Gaussa-Ostrogradskiego obliczyć całkę powierzchniową 1= jjf 4xⁱdydz-\-4yⁱdxdz—6z^Ądxdy, gdzie o — całkowita powierzchnia walca (rys. 197) danego w zad. 906(2).

Rozwiązanie. Porównując daną całkę z lewą stroną wzoru (3) widzimy, żc P = 4.v³, Q — 4y\ R = —6z*. Następnie znajdujemy pochodne P'_x = I2x², Q’_y — 12y~, R’_x = —24z³ i podstawiamy je do prawej strony wzoru (3). W ten sposób zamiast danej całki powierzchniowej po zamkniętej powierzchni a otrzymaliśmy całkę potrójną po obszarze G, ograniczonym przez tę powierzchnię

7 — 12 f f f (x²+y²-2z³)dxdydz

G

Całkując najpierw względem z, a potem przechodząc do współrzędnych ■biegunowych, znajdujemy

h

/= 12 f f dxdy f (x²+y²—2z^}')dz — ^cxy    °

= 12    || j" (x²+y²)z— -yT dxdy =

= 12 f J |e²/! - od(fdo =

eśp

2n    a

O o

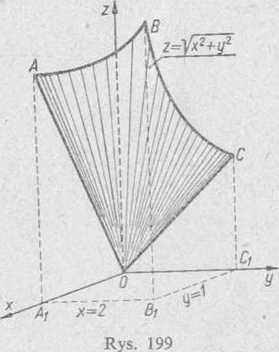
909. Korzystając ze wzoru Stokesa obliczyć całkę krzywoliniową K — 2

= j e^xdx^Jrz(x²+y²)²dy+yz^dz, gdzie / — zamknięta linia OCBAO

— 12/j j df | [p¹ —-^^jdo == 6nd¹h(a^l—h^y)

A    A '    ^J

(rys. 199) przecięcia się powierzchni z — \ x^2jry² z płaszczyznami x = 0, = 2, y = 0, y = 1.

2 2

Rozwiązanie. Porównując całkę K z prawą stroną w'zoru (4),

widzimy, że P = e^x, Q = z(x²-]-y²) , R — yz³. Następnie znajdujemy

3

pochodne: p; = P^ = 0, 0; = 3.vz    g: = (**+/) * , P* = 0,

397