1tom177

7. ELEKTRONIKA 356

-im-n

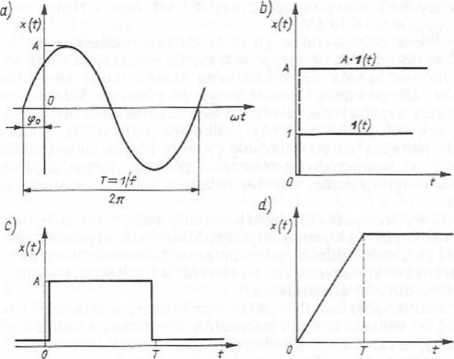
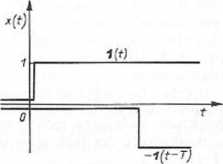
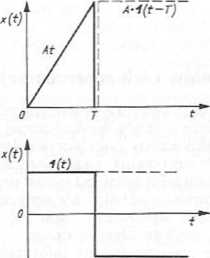
Rys. 7.31. Przykłady reprezentacji czasowej modeli sygnałów deterministycznych: a) przebieg harmoniczny; b) skok jednostkowy; c) impuls prostokątny; d) wzrost liniowy ograniczony

—    skok jednostkowy (Heaviside’a)

x{t) = l(t); skok o amplitudzie A: x(t) = A ■ 1 (t)

—    impuls prostokątny

x(t) = /l[l(t)-l(£)(t-r)]

—    wzrost liniowy ograniczony

*(£) = Y t [i w - a w (t - r)]+/i • i (t - n

W elektronice sygnałowej bardzo często dogodniejsza praktycznie jest reprezentacja częstotliwościowa x(co), to = 2nf. Obie reprezentacje są równoważne, jeśli są powiązane przekształceniem Fouriera

(7.29)

2    + CC

x(t) = — f eⁱ"F(joj)dw

2n *

dla przebiegów nieokresowych jednoznacznych o skończonej energii, a dla przebiegów jednoznacznych okresowych szeregiem Fouriera w postaci trygonometrycznej

+ X

x(r) = n₀+ Z e,^c°s(a>.t+9»J;    i₀<t<t₀ + T    (7.30a)

tt— 1

(7.30b)

lub w postaci wykładniczej x(r) = I A.&°ri

n= ^— eC

Widmem zespolonym przebiegu x(t) nazywa się zbiór amplitud zespolonych A„ na osi częstotliwości. W praktyce stosuje się częściej rozdzielenie widma na amplitudowe |zł_n(co)| i fazowe e>„(co). Widmo przebiegów okresowych jest widmem prążkowym (dyskretnym), nieokresowych — ciągłym.

Istotnym parametrem charakteryzującym widmo sygnału jest przedział częstotliwości [c)_d, C0g], zwany pasmem częstotliwości lub szerokością widma sygnału: W =^f(co₉ — a>_d) rad/s

lub B

def

W . 2n

Hz. Wybór częstotliwości granicznych jest arbitralny i związany z pojęciem

mocy sygnału — pasmo określa decydującą część mocy sygnału. Przykłady widma dwustronnego amplitudowego podano na rys. 7.32.

^a)

*{*)

*(*)

-r/Z 0 r/Z t

Ml.

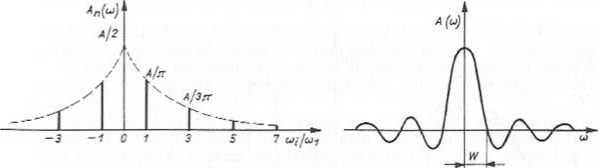
Rys. 7.32. Przykłady widma amplitudowego dwustronnego: a) widmo prążkowe ciągu impulsów prostokątnych; b) widmo ciągłe impulsu prostokątnego

Widmo mocy sygnałów okresowych napięcia lub prądu

^p = ^: f x²(t)dt= Y. = al+Y^ti    (7-31)

¹ -772    ii=-x    “

Jeśli a₀ > 0, to m_d = 0 — sygnał dolnopasmowy.

Jednym z kryteriów określenia a>_g jest wartość co, przy której obwiednia mocy zmniejsza się do połowy wartości maksymalnej. Można też przyjąć za kryterium co

1

zmniejszenie sie widma amplitudy \A(co)| do wartości 0,707 = —— A_m„ (spadek o 3 dB).

Jeśli obwiednia przecina oś odciętych, to co₅ odpowiada pierwszej zerowej wartości obwiedni widma amplitudowego mocy.