238 239

238 Metody wielokryterialne

238 Metody wielokryterialne

Chcąc uzyskać kompletny ranking za pomocą metody Promcthee II. oblicza

my dla każdego wariantu decyzyjnego xe A przepływ netto, korzystając z wzoru: 4>(x) = $⁺(x) - 0~(x).

Dla kolejno rozpatrywanych wariantów mamy:

cp(a) = 0>^ł(a) - O-(a) = 0,417 - 0,199 = 0,218, d>(b) = <I>'(b) - d)-(b)= 0,175 - 0,384 = -0,209,

<D(c) = <l>^ł(c) - 4>-(c) = 0,326 - 0,242 = 0,084,

O(d) = d)⁺(d) - 0>-(d)= 0,324 -0,417 = -0,093.

Otrzymujemy następujący ranking rozpatrywanych wariantów decyzyjnych.

Najlepiej ocenionym wariantem jest wariant a, drugie miejsce zajmuje wariant c. Warianty te różnią się stosunkowo nieznacznie względem preferencji decydenta, zdecydowanie gorzej ocenione są dwa pozostałe warianty, przy czym wariant d został lepiej oceniony niż wariant b.

4.6.3. Metoda Ełectre I

Podobnie jak w przypadku metody Promethee II, rozpatrujemy zbiór A złożony z n wariantów decyzyjnych, oceniany ze względu na k maksymalizowanych kryteriów. Każdemu kryterium decydent przypisuje dodatnią wagę w_k, odzwierciedlającą jego ważność. Przyjmujemy, że wagi te sumują się do jedności.

Mając dane dwa warianty decyzyjne x oraz y, ustalamy, czy ze względu na kryterium/* wariant x oceniany jest nie gorzej niż wariant y. Obliczamy w tym celu wskaźnik przewyższania:

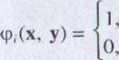
gdy /(x) $*/,(y) w przeciwnym przypadku.

(4.7)

Z kolej możemy zapylać o stopień przewagi wariantu x nad wariantem y, rozumiany jako suma wag tych kryteriów, dla których wartości dla wariantu x są nie mniejsze niż dla wariantu y. Obliczamy w tym celu współczynnik zgodności:

k

c(x, y) = Z w, <p,(x, y).

(4.8)

Warunek zgodności spełniony jest wówczas, gdy współczynnik zgodności jest nie mniejszy niż wartość podanego przez decydenta progu zgodności ,v e 10,5; 1J. Jeżeli para wariantów x oraz y spełnia warunek zgodności, należy jeszcze sprawdzić, czy spełniony jest warunek braku niezgodności. Chodzi o to, by X wyeliminować sytuację, w której co prawda spełniony jest warunek zgodności, lecz f

przynajmniej jedno z kryteriów przeważającego wariantu

wartość. Wykrycie takiego przypadku możliwe jest dzięki zastosowaniu progu weta, którego poziom zadany jest przez decydenta.

Stosując metodę Electre I, możemy wyróżnić następujące etapy:

1.    Wyznaczenie wszystkich par wariantów decyzyjnych, spełniających warunek zgodności na zadanym przez decydenta poziomie Zbiór ten nazywamy zbiorem zgodności i oznaczamy jako C_v.

2.    Znalezienie wśród nich tych par, dla których należy zastosować zasadę weta. Zbiór ten nazywamy zbiorem niezgodności i oznaczamy jako D_v.

3.    Określenie relacji przewyższania S(.?, w) jako zbioru tych par wariantów decyzyjnych, które spełniają warunek zgodności i jednocześnie spełniają warunek braku niezgodności, czyli

S(s, v)-C_an D„    (4.9)

przy czym symbol D, oznacza uzupełnienie zbioru D,. do całej przestrzeni.

4.    Konstrukcję grafu zależności między wariantami.

Przykład 4.I6⁸

Rozpatrujemy dyskretny problem wielokryterialnego podejmowania decyzji w którym 9 wariantów decyzyjnych jest ocenianych ze względu na 4 kryteria. Oceny wariantów decyzyjnych względem kryteriów przedstawia tablica 4.25.

Tablica 4.25

Warianty	Kryteria
	/.	f?	h	U
a'	3	6	7	8
a^J	5	4	7	9
a’	10	2	5	4
a"	4	8	5	2
a^5	2	5	u	1
a"	9	6	3	6
a^7	4	9	7	6
a"	1	7	9	10
a"	5	3	6	4

W wyniku analizy preferencji decydenta przyjęto, że dla kolejnych kryteriów progi weta są stałe i wynoszą odpowiednio v, =5, v₂- 7, w, = 6, v₄ = 5, zaś współczynniki wagowc przyjmują wartości następujące: w, = 0,08, w₂ = 0,33,

" Przykład (en, opracowany przez M.Nowaka zaczerpnięto z książki pod red. T. Trzaskalika, Metody wielokryterialne na polskim rynku finansowym, PWF., Warszawa 2006 (przykład 2.10).