2016

BADANIE OBWODÓW ll-go RZĘDU Pomiary w obwodzie BLC

Obwód RI .C przedstawia poniższy rysunek

C

L, R_l

Równanie obwodu

L⁽-~+ Ry ■ m+4■ frfttf + ^u<(°) = e(i)

^{dt    c} i

d^:i(0 _| R_x di(t) _| I    1 fłe(t)

dr    L dt LC ' L dt

^A-(y) ~    u„(t)=Ri(t)

Przyjmujemy:

e(t) = E = const, u(0) = 0. i(0) = 0, R_Z=R+R_L

Wielkości obliczone teoretycznie 2E

i(t) = I ■ e sin(u ■ 0    = —7=    T =

IV- A    w

a = —    co= — yP-A.    /!. = /„ e ¹ A, = /, e

21 2 " *

i(l) = C, • <?^v' + C, ■ e^,,t' C. = -C, =

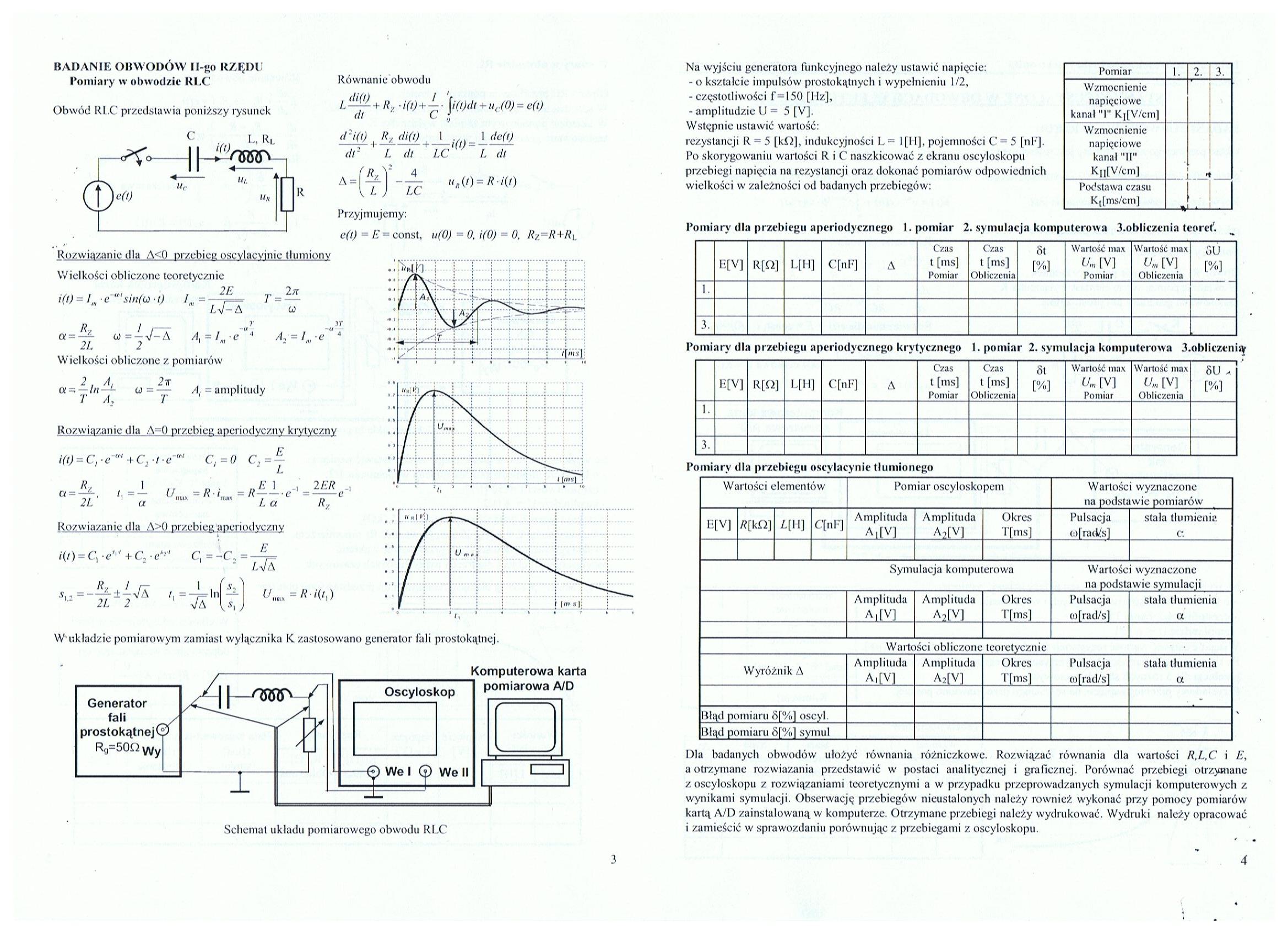
Rozwiązanie dla A<0 przebici; oscylacyjnie tłumiony

2/r

Ry    I

21

Wielkości obliczone z pomiarów

2 . A,    2ir    ,

«=; — /// w =— /I = amplitudy T A_:    T ‘

Rozwiązanie dla A=0 przebieg aperiodyezny krytyczny i(l) = C., e +C,    e"' C, = 0 C, = --

/?,    I    _ . _nE I    2 ER

a = —,    r, =— U„_m=R-i,_lt,=R---e =-e

2L    a    La R_y

Rozwiązanie dla A>0 przebieg aperiodyezny

E

/.Va

W układzie pomiarowym zamiast wyłącznika K zastosowano generator fali prostokątnej.

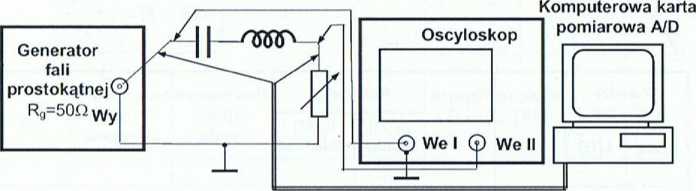
Schemat układu pomiarowego obwodu RLC

Na wyjściu generatora funkcyjnego należy ustawić napięcie:

Pomiar	1.	2.	3.
Wzmocnienie napięciowe kanał "1" K|[V/cm|
Wzmocnienie napięciowe kanał "II" K||[V/cm]		*
Podstawa czasu K([ms/cm]	—		_

-    o kształcie impulsów prostokątnych i wypełnieniu 1/2,

-częstotliwości f=15() [Hz],

-    amplitudzie U = 5 [V],

Wstępnie ustawić wartość:

rezystancji R = 5 [kii], indukcyjności L = I [I I |, pojemności C = 5 |ni']. Po skorygowaniu wartości R i (' naszkicować z ekranu oscyloskopu przebiegi napięcia na rezystancji oraz dokonać pomiarów odpowiednich wielkości w zależności od badanych przebiegów:

Pomiary <lln przebiegu aperiodycznego I. pomiar 2. symulacja komputerowa 3.obliczenia teoret.

	EM	R[0]	L[H]	C[nF]	A	Czas t [ms] Pomiar	Czas t [ms] Obliczenia	8t [%]	Wartość max v,„ [ V ] Pomiar	Wartość iuax Um M Obliczenia	oU [%]
i.
3.

Pomiary dla przebiegu aperiodycznego krytycznego 1. pomiar 2. symulacja komputerowa 3.obliczeimy

	E[V|	R[0]	L[H]	C[nF]	A	Czas t [ms] Pomiar	Czas l [ms] Obliczenia	8t [%]	Wartość niax U,„ [V] Pomiar	Wartość inax um [V] Obliczenia	8 U ^ [%]
1.
3.

Pomiary dla przebiegu oscylacynie tłumionego

Wartości elementów				Pomiar oscyloskopem			Wartości wyznaczone na podstawie pomiarów
E[V]	/ć[k£2]	/-[U]	C[nF]	Amplituda A i [ V ]	Amplituda A,rvi	Okres 1 [ms]	Pulsacja tofrad/s]	stała tłumienia c.
Symulacja komputerowa							Wartości wyznaczone na podstawie symulacji
				Amplituda A i [V]	Amplituda A?[ V ]	Okres T[ms]	Pulsacja cofrad/sl	stała tłumienia a
Wartości obliczone teoretycznie
Wyróżnik A				Amplituda A, M	Amplituda A2[V]	Okres • [ ^,T,s]	Pulsacja tofrad/s]	stała tłumienia a
								. -
Błąd pomiaru 8[%] oscyl.
Błąd pomiaru 8f%] symul

Dla badanych obwodów ułożyć równania różniczkowe. Rozwiązać równania dla wartości R.L.C i E, a otrzymane rozwiązania przedstawić w postaci analitycznej i graficznej. Porównać przebiegi otrzymane z oscyloskopu z rozwiązaniami teoretycznymi a w przypadku przeprowadzanych symulacji komputerowych z wynikami symulacji. Obserwację przebiegów nieustalonych należy również wykonać przy pomocy pomiarów kartą A/D zainstalowaną w komputerze. Otrzymane przebiegi należy wydrukować. Wydruki należy opracować i zamieścić w sprawozdaniu porównując z przebiegami z oscyloskopu.

4