2022

Wzory do obliczeń:

R„ =

e=u°_m=u

li =

U» = u_v

, dlii

A, =

= o

/:

li,

(K + KY

U = /(/„) = (/(/„) = £ - /?„. • /„

Na podstawie pomiarów obliczamy opór /?ooraz moc l\> według odpowiednich wzorów.

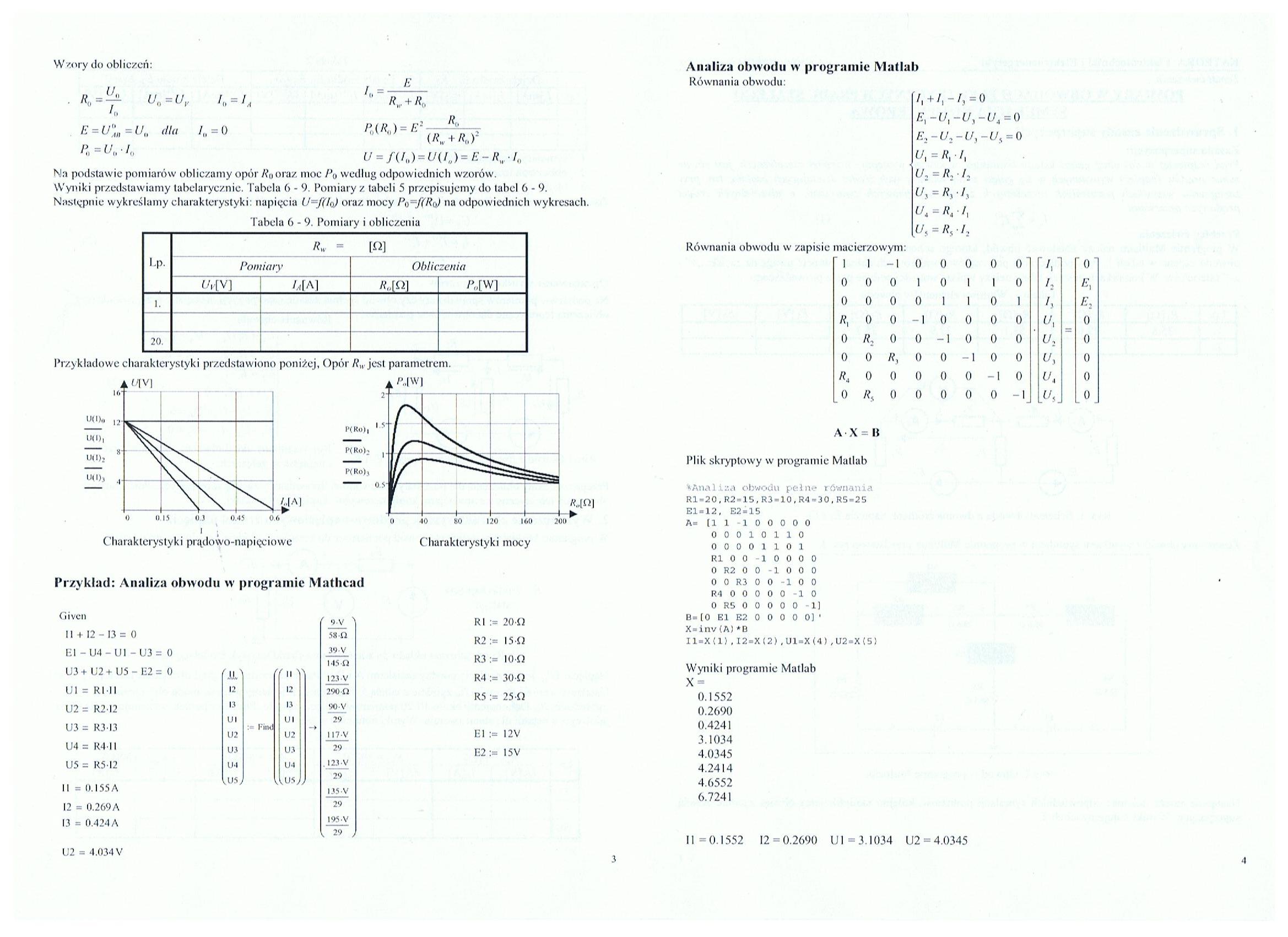
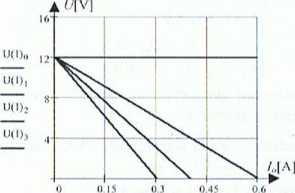
Wyiriki przedstawiamy tabelarycznie. Tabela 6 - 9. Pomiary z tabeli 5 przepisujemy do tabel 6 - 9. Następnie wykreślamy charakterystyki: napięcia U=f(lo) oraz mocy Po—f(Ro) na odpowiednich wykresach.

Tabela 6 - 9. Pomiary i obliczenia

	Rw = ffl]
l.p.	Pomiary	Obliczenia
	t/,[V] Ia[A]		/>„[W]
1.
20.

Przykładowe charakterystyki przedstawiono poniżej. Opór A’„ jest parametrem.

Charakterystyki prądowo-napięciowe

Przykład: Analiza obwodu w programie Mathead

Givcn

11 + 12- 13 = 0 El -U4 - Ul - U3 = 0 U3+ U2+ U5-E2= 0 Ul = Rll I U2 = R2-I2 U 3 = R3-I3 U4 = R4II U5 = R5-I2

11    = 0.155 A

12    = 0.269 A

13    = 0.424 A

CdC

12

13

Ul

U2

U3

U-l

,us,

((II

I-ind

\\

12

13

Ul

U2 U 3 U-l

' 9V '

58 n 3'jv 145 -n 123 V 290 £2 90 .y 29

II7-V 29

■^l23-v 29

I35-V

29

195 • V , 29    ,

Rl := 20 S2 R2 := 15 0 R3 := 10 O R4 := 30-£2 R5 := 25-S2

El := I2V E2 := 15 V

U2 = 4.034 V

Analiza obwodu w programie Matlab

Równania obwodu:

/| +1\ ~ h - 0 E\ ~U\ - U, -U_Ą = 0 E₂-U₂-U,-U>=0 (/,=«,/,

^U2 = /,

Uy =/?,•/,

U* = *4 A Uy=Ry'I₂

Równania obwodu w zapisie macierzowym:

■ 1	1	-1	0	0	0	0	0 "				' 0 '
0	0	0	1	0	1	1	0		L
0	0	0	0	1	1	0	1		h		£,
	0	0	-1	0	0	0	0				0
0	IL	0	0	-1	0	0	0		U;		0
0	0	*,	0	0	-1	0	0		</,		0
*4	0	0	0	0	0	-1	0		U,		0
0		0	0	0	0	0	-1		U}_		0

A X = B

Plik skryptowy w programie Matlab

'‘■Analiza obwodu pełne równania ri=2o,r2=is,r3»io,r4.~3o,r5.=25 El=12, E2 = 15 A= [11-100000 00010110 00001101 R1 00-10000 0R2 00-1000 0 0 R3 0 0 -1 0 0 R4 00000 -10 0 R5 0 0 0 0 0 -1]

B= [0 El E2 0 0 0 0 0) '

X = inv (A) *13

Il-X(l),I2»X(2),U1=X(4),U2-X(5)

Wyniki programie Matlab X =

0.1552

0.2690

0.4241

3.1034

4.0345

4.2414

4.6552

6.7241

II =0.1552    12 = 0.2690 UI = 3.1034 U2 = 4.0345

4