33(1)

Jeśli na przykład energia kinetyczna cząstki wynosi początkowo 5 J. a w wy. niku działania siły cząstka zyskuje 2 J (całkowita praca jest dodatnia), lo końcowa energia kinetyczna cząstki wynosi 7 i. Jeśli natomiast w wyniku działania siły cząstka traci 2 J (całkowita praca jest ujemna), to końcowa energia kinetyczna cząsfki wynosi 3 J.

i/sprawdzian 1 : Cząstka porusza się wzdłuż osi x. Czy energia kinetyczna cząstki

wzrośnie, zmaleje, czy pozostanie bez zmiany, gdy prędkość cząstki zmieni się: a} z -3 tn/s na - 2 m/s, h) /. — 2 m/s na 2 m/s? c) Czy praca, wykonana nad cząstką, w każdym z tych przypadków jest dodatnia, ujemna, czy równa zeru?

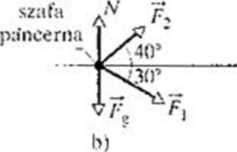
szpiedzy przesuwają szafę pan-ir ii. b) Diagram sił działających

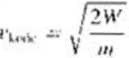
/2(153.4 J) V (225 kg)

1.17 m/s

Przykład 7.2

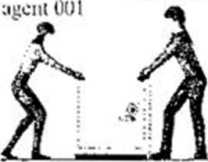
:\u rysunku 7.1a przedstawiono dwóch szpiegów przemysłowych. pr/CNUwających s/alę pancerną prosto d<» 'wej ciężarówki. Szala ma masę 225 kg i była początkowo w spoczynku. a jej przemieszczenie <1 do ciężarówki ma wartość 8.5 m. Agent 001 pcha szafę siłą T\ o wartości 12 N. skierowaną pcnl kątem 30 w dól od poziomu a agent 002 ciągnie ją siła /Ą o wartości 10 N. skierowaną pod katem -to w górę po/ionm. Szafa |X»rusza się ]>o p\>dladzo !uv tarcia, a wartości t kierunki sil. jakimi działają na nią obaj agenci nie zimcniaią się podczas ruchu szafy.

agent 002

0

a)

Rys. 7.4. Przykład 7.2. a) Dwaj eerną. przemieszczając ją o weku na tę szafę ai laką całkowitą pracę nad szalą wykonają siły /', i / • |xulc/as jej pi zcmtcszczania o wektor </?

ROZWIĄZANIE:

Zauważ, że:

O—nr 1. Całkowita praca wykonana nad szafą przez, dwie siły jest równa sumie prac wykonanych przez każdą z nich

O—r 2. Szalę możemy potraktować jak cząstkę, a siły są stale co do wartości i kierunku, dlatego też do obliczenia tych prac możemy zastosować wzór (7.7) (W = /-'</cos<p) lub wzór (7.8) (IV = /•’ • cl). Wybieramy wzór (7.7). gdyż dane są wartości i kierunki sil. Praca wykonana przez silę ł'\ wynosi:

IV, = F,</cos«/>, = (12 N)(8.5 m)(cos 30 ) = 88.33 J.

;t praca wykonana przez siłę F> jest równa

Wy = Fydcosfc = (10 N)(8.5 m) (cos 40 ) = 65.! l j Całkowita praca U' w v nosi zaiem:

W = IV, -I- W₂ = (88.33 U -ł- (65.11 J) = 153.4 J 153 J.

(odpowiedź)

Tak więc w trakcie prze mieszczan i u szafy pancernej o 8.5 _m s/picd/.y zwiększyli jej energię kinetyczną o 153 J.

b) Wyznacz pracę U... wykonali:) nad szalą podczasjci przesuwa-nia przez silę ciężkości oraz pracę U\-, wykonaną przez silę normalną »V. działającą na szalę ze strony podłogi.

ROZWIĄZANIE

O—r Obie te siły są stale co do wartości i kierunku, więc wy. konaną przez nie pracę można ohlic/.yć ze wzoru (7.7). Wartość siły ciężkości wynosi my». otrzymujemy więc:

= ntfitlcos 90 = mt!(l(0) - 0    (odpowiedź)

i podobnie:

= .Vcl cos 90 = .67/(0) = 0.    (odpowiedź)

Takiego wyniku należało się spodziewać. Te dwie siły są prostopadłe do wektora przemieszczenia szafy, a więc wykonują one nad nią zerową pracę, czyli nie dostarczają szalio ant nie odbierają :kJ niej żadnej energii e) Szala jest początkowo w spoczynku, laka jest wartość jej prędkości /i.,_llA po przemieszczeniu jej o 8.5 iii?

ROZWIĄZANIE:

O—r Prędkość szafy pancernej ulega /.mianie, gdyż w wyniku przekazania jej energii przez siły F, i / > zmienia się jej energia kinetyczna. Aby otrzymać związek prędkości /. pracą, zastosujemy rów nania (7.10) i (7.1). co daje:

^w - ^/,;v^ -    - §""W

Prędkośe początkowa u,**, jest równa zeru. a — jak juz wiemy — wykonana została praca, równa 153.4 J. Wyznaczając z powyższego równania i podstawiając dane liczbowe, otrzymujemy: (odpowiedź)

146

7. Energia kincłyczna i praca

przykład 7.3

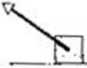
podczas burzy skrzynio ślizga się po gładkiej. pokrytej olejem nawierzchni parkingu, doznając przemieszczenia d = (-3 m)i. przez cały czas towarzyszący burzy wiatr działa na skrzynię silą: jr - (2 N)i + (-6 N)j. Omawianą sytuację oraz układ współrzędnych przedstawiono na rysunku 7.?.

y

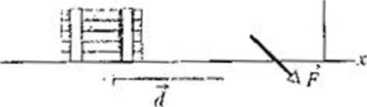
Rys. 7.5. Przykład 7.3. Stała siła /• spowalnia ruch skrzyni doznającej przemieszczeniu d

a) Ile wynosi praca wykonana przez silę wiatru nad skrzynią podczas jej przemieszczaniu?

ROZWIĄZANIE:

O—» Ruch skrzyni można opisać jako ruch cząstki, a siła wiatru jest w czasie rudni skrzyni stała co do wartości i kierunku, dlatego leż do ohłk /ema prac\ możemy zastosować wzór 17 7 > (IV' = /-‘r/eos</>) lub wzór (7,X) (IV — /•' • d>. Wybieramy wzór (7.8), gdyż. wektory /•' i d zapisane są przy użyciu wektorów jednostkowymi i. Oir/.ymujemy:

ir - ż^: •</-•* li? N)i -< o N »il Ił - 3 imi|.

Jedynie następująco iloczyny skalarne wektorów jednostkowych są różne od zera: i ■ i. i • i oraz k k (patrz dodatek £). Wolicc tego mamy:

W = (2 N)(—3 in)i • i + ( 6 N)(-3 m)j • i

= ( -5 J)(l) + 0 = — 6 J.    (odpowiedź)

Tak więc siła wiatru wykonała nad skrzynią pracę ujemną o wartości 0 J. czyli zmniejszyła energię kinetyczną skrzyni o 6 J.

b) Ile wynosiła energia kinetyczna skrzyni po przemieszczeniu jej o 7l. jeśli na początku ruchu była ona równa 10 J?

ROZWIĄZANIE:

O—nr Siła wiatru wykonała nad skrzynią pracy* ujemną, a zatem zmniejszyła jej energię kinetyczną. Korzystając ze związku pracy ze zmianą energii kinetycznej w |x>siaci wzoru (7.11). mamy:

Bi k,,k = Er ,hv/ 'h W = 110 J) -r <— 6 J) sr 4 J. (odpowiedź)

finergiu kinetyczna skrzyni zmniejszyła się sio wartości -4 1. a zatem ruch skrzyni zastał spowolniony.

s

5PRAWP7!/\M 7 \j., rysunku przedstawiono cztery przypadki. w których na pudełko ślizgające się Ik*z. tarcia po podłożu w prawą stronę na odległość </ d/iałąią rożne sil). Wartości tych sil są jednakowe, a ich kierunki pokazano na rysunku.

I•'.szereguj te przypadki według pracy wykonanej nad pudełkiem |xk]o/us lego pr/omies/tzenia. ml najbardziej dodatniej | do najbardziej ujemnej.

Iil_    O—o

a)    b)    c)    d)

7.4. Praca wykonana przez siłę ciężkości '

link

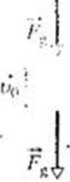
d

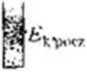
Rys. 7.6. Pomidor o masie ni. rzucony w górę z prędkością początkową ó, zwalnia do prędkości u. doznając przemieszczenia d. ponieważ działa na niego siła ciężkości F_v. Wskaźnik energii kinetycznej pokazuje zmianę energii kinetycznej ciała od wartości    < —

3‘mi^) do F.i (- \mtr)

Ro/.patr/yim tera/ przypadek. gdy praca jest wykonana nad ciałem przez szczególny rodzaj siły. mianowicie pr/.cz działającą na nie silę ciężkości. Na rysunku 7.6 przedstawiono pomidora o masie mi, rzuconego w górę z prędkością początkową i\_h a więc mającego początkowo energię kinetyczną Ekpoc/ “ iMitijj. Gdy pomidor wznosi sic, jego ruch jest spowalniany przez silę ciężkości F_?. izn. jego energia kinetyczna maleje, gdyż siła ciężkości wykonuje nad nim pracę.

Załóżmy, że możemy potraktować pomidora jako cząstkę i do wyznaczenia pracy wykonanej podczas przemieszczenia cl skorzystajmy z równania (7.7) (W = Pd cos4>)- W miejsce wartości siły F podstawiamy wartość siły tzn. mg. Zatem praca wykonana przez siłę ciężkości wynosi:

Wj, “ mgdeas <£ (praca wykonana przez silę ciężkości).    (7.12)

7.4. Praco wykonana przez siłę ciężkości 147