3tom155

4. STACJE ELEKTROENERGETYCZNE 312

W przewodach szynowych wiązkowych odstęp między przewodami wiązki utrzymują odstępniki. W chwili wystąpienia zwarcia przewody składowe wiązki zaczynają gwałtownie się przyciągać, powodując zwiększenie ich naciągu po raz pierwszy (w przewodach pojedynczych zjawisko to nie występuje). Przy zwarciu trójfazowym i płaskim ułożeniu przewodów, w wyniku oddziaływania na siebie różnych faz, przewody faz skrajnych w pierwszej chwili wychylają się na zewnątrz (po łuku 2-3 na rys. 4.39). W tym czasie przewód fazy środkowej wychyla się niewiele. Przy największym wychyleniu się przewodów (3 na rys. 4.39) występuje w nich drugi szczyt naciągu, pochodzący od działania siły odśrodkowej. Po wyłączeniu prądu zwarciowego przewody nadal poruszają się pod wpływem działania siły bezwładności, przy czym w pewnej chwili następuje opadnięcie wzniesionego przewodu, powodujące trzeci szczyt naciągu (5 na rys. 4.39).

Obliczenia dokładne naciągu zwarciowego w przewodach giętkich są skomplikowane, ze względu na nieliniowość zachodzących zjawisk. Do celów praktycznych norma PN-90/E-05025 [4.19] podaje wzory uproszczone, słuszne dla przęseł o długości nie większej niż 20 m. W przypadku przęseł dłuższych należy korzystać z metod dokładniejszych.

Rozróżnia się: naciąg F, — występujący w czasie trwania zwarcia oraz naciąg F_f — występujący po zwarciu, gdy przewody opadną do pozycji wyjściowej.

Naciąg zwarciowy F„ w niutonach, pojedynczego przewodu oblicza się ze wzoru

(4.15)

F,= FM + ętl>)

gdzie: F_st — naciąg statyczny przewodu, N; ij/ — współczynnik odczytany z rys. 4.40; (p — współczynnik obliczony wg wzoru

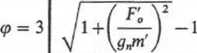
w którym: g„m‘ — siła ciężkości przewodu, N/m; F’₀ — siła jednostkowa, N/m, działająca na przewód fazy zewnętrznej pod wpływem prądu zwarcia, obliczona wg wzoru

F₀ = 0,15

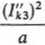
(4.17)

przy czym: /('₃ — wartość początkowa prądu zwarcia trójfazowego (wartość skuteczna), kA; a — odległość między osiami przewodów różnych faz, m.

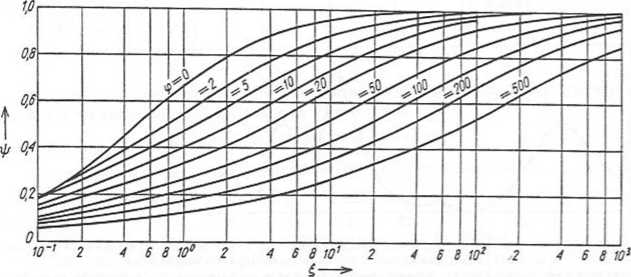
Rys. 4.40. Współczynnik \p do obliczania naciągu zwarciowego, wg [4.19]

Wartość ć niezbędną do odczytania z rys. 4.40 wartości współczynnika ip oblicza się wg wzoru

(4.18)

(m'l)²    400

i 100

10S1 ~Ta

gdzie: l — odległość między osiami punktów zamocowania przewodów fazowych (konstrukcji wsporczych), m;S — sztywność konstrukcji wsporczych, N/mm (jeśli wartość S nie jest znana, to można przyjąć S = 100 N/mm); E — moduł Younga, N/mm²; A — przekrój przewodu, mm².

K

Naciag F_f po zwarciu oblicza się wówczas, gdy —— > 0,6, wg następujących wzorów:

gjn’

Ff=FM0 /lA V	jeśli	fN V 1 <35
Fj = F ,t60 v'^/*+	jeśli	gjn
gdzie Fa40 — naciąg statyczny przewodu w ti

(4.19)

Podane wzory na obliczanie naciągów nie uwzględniają zwiększenia naciągu spowodowanego „sklejeniem się” przewodów składowych wiązki. Zaleca się taką budowę wiązki, aby przyrost naciągu wskutek wzajemnego oddziaływania jej przewodów był nie większy niż 10% naciągu F, obliczonego wg wzoru (4.15) [4.6]. Warunek ten spełnia np. wiązka, w której odstęp między osiami przewodów wynosi 2,5d, a odległość między odstępnikami jest nie mniejsza niż 70d (d — średnica przewodu składowego wiązki). W przypadku tak zbudowanej wiązki naciąg zwarciowy przewodów można przyjmować jako równy 1,1F„ gdzie F, oblicza się wg wzoru (4.15).

Działanie sił elektrodynamicznych powinno być uwzględniane podczas projektowania zarówno konstrukcji wsporczych, jak i połączeń, w których przewody są mocowane bezpośrednio do aparatów lub izolatorów, gdyż wartości sił przy zwarciu mogą być znacznie większe od wynikających z obciążeń statycznych. Obliczone siły dynamiczne nie mogą być większe od wytrzymałości konstrukcji, aparatów lub izolatorów, określonej przez producenta.

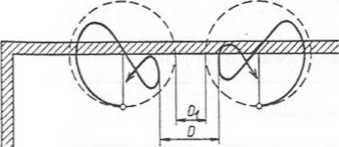
Rys. 4.41. Tory ruchu przewodów przy zwarciu dwufazowym, wg [4.6]

D — odstęp pomiędzy przewodami fazowymi przy wychyleniu podczas zwarcia, D_y — odstęp przybliżony

Ruch przewodów giętkich pod wpływem sił elektrodynamicznych powoduje wzajemne zbliżenie się przewodów różnych faz oraz zbliżenie przewodów do konstrukcji uziemionych. W projektowaniu decydujące znaczenie dla ustalenia odległości między przewodami ma przypadek zwarcia dwufazowego, gdyż wówczas występuje największe zbliżenie przewodów (rys. 4.41). Dokładne obliczenie odległości D wymaga żmudnych rachunków. W praktyce wystarcza założenie, że ruch przewodów' odbywa się po okręgu o promieniu