818

wszystkich n* wokscli dokonujemy pomiaru osoboo Jest lo metod* FON AR. zaproponowana przez R. Damadiana. Wymaga ona oczywiście długiego czasu (10 h) do uzyskam* obrazu i dlatego nie ma praktycznego znaczenia. Ze względu na potrzebę skracania tego czasu sygnały FID rejestrowane s jednocześnie z n wokscli jednego paska, a nawet n^: wokseli całej płaszczy zny. Specjalne metody, z udziałem transformacji Fouriera, pozwalają rozdzielić informacje z poszczególnych wokseli i zrekonstruować z nich obraz. W standardowych tomografach NMR stosuje się najczęściej metodę d*'u*^jmaro**) transformacji Fouriera (2D FF). W metodzie tej rozróżniamy (kodujemy) woksele w jednym kierunku (y) przez częstoić. w be-runku prostopadłym Ul przez fazf. Sposób postępowania jest następujący. Wybieramy gradientem C_t czułą na rezonans warstwę obrazowania i włączamy impuls RP90° o częstości rezonansowej Czas trwania impulsu jest taki. że wektor magnetyzacji zajmie położenie w płaszczyźnie r.vi będzie stanowił składową (składową poprzeczną). Wektor magnetyzacji wszystkich rczonujących jąder w wybranej warstwie, wiruje w płaszczyźnie x_%y z częstością Włączamy teraz drugi gradient pola. powodujący wzrost indukcji pola. na przykład wzdłuż kierunku y, oznaczony u , Wektor magnetyzacji rozdzieli się wzdłuż osi y na składowe, które będą różnić się częstością wirowani* (ttl- yB) W sygnale FID otrzymamy widmo częstości, przy czym różnica częstości będzie proporcjonalna do y (odległość jest kodowana przez częstość). Po fourierowskiej transformacji sygnału FID otrzymujemy jednowymiarową projekcję obrazu (ryc. 25.11).

Amplituda sygnału NMR na poszczególnych częstościach pochodzi z wszystkich re/onujących jąder położonych w pasku o grubości Az, szerokości Ay i całej

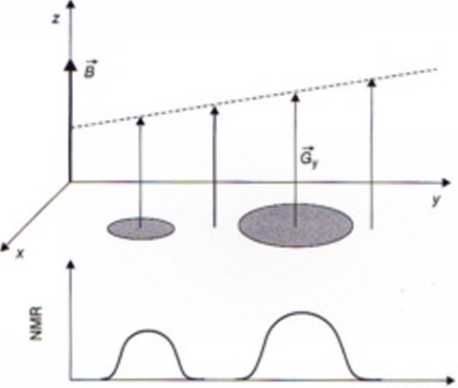
Ryc. 25.11. Jednowymiarowa projekcja sygnałów NMR dwóch obiektów zawierających jądra wodoru, zlokalizowane w płaszczyźnie t^e

818