Capture144

0.489/(4 - I)

(I -0.489VT26 41

Jest to ten uin stosunek F. z Zaokrągleniem do części dziesiętny, |, otrzymany u tabeli 15.3. Analiza wariancji i stosunek korci* ś|t,_v nymi sposobami postępowania i prowadzą do tych samych wyników’’ ^H

15.11. Założenia leżące u podstaw analizy wariancji

Test F. przedstawiony w tym rozdziale, opiera sic na wielu zało/cnijch \\ sprawą jest charakter tych załozeń. a także to. w jakim stopniu ich _nievM. ^ prowadzi do wyciśnięcia fałszywych wniosków. Zagadnienie to omawia, niższym rozdziale, jednak spełnienie podobnych zalozcń jest konieczne _r,,.. . przypadku planów dwuczynnikowych i trójczynnikowych. omamionych ..    *

następnych rozdziałach. Założenie dodatkowe, wymagane pr/y .indi/ic p nych pomiarów, zostanie omówione w rozdziale 19.

Założenie pierwsze wymaga, by pomiary zmiennej zależnej muły rwU:j_r., I malny w obrębie każdej grupy Założenie drugie nakazuje, by wanancjj pr ., była jednakowa we wszystkich grupach Właściwość tę określamy mianem i-,, rodności (homogcniczności) wariancji. Założenie trzecie to statystycznj mc£« ność pomiarów w obrębie grupy.

Test F znany jest jako całkiem odporny na niespełnienie zalo/cnu n<>nmL*«> | ści rozkładu. Jeżeli nie ma podstaw, by podejrzewać skrajne odstępstw j ,*j malności. to prawdopodobne jest, ze wyciągnięte wnioski nie będą poważnie I kształcone Przy dużych próbach normalność rozkładu można sprawdzić z u p odpowiedniego testu, na przykład testu zgodności chi-kwadrat W eksperu kontrolowanych jednak próby prawie bez wyjątku są małe i w takich przyj zazwyczaj nie jest możliwe ścisłe wykazanie odchyleń rozkładu wyników od ar ma! naści.

Powstaje tu pewna trudność, związana z faktem, że normalność r»/kłjćin»_:l magana jest w obrębie ka/dej grupy. Należałoby zatem badać ja osobno dh grupy, jeżeli wszystkie grupy nie mają tego samego rozkładu Jeżeli wvy> grupy mają ten sam rozldsd, z wyjątkiem ewentualnych różnic dotyczących wł nich. to średnic z grup można odjąć »xl pojedynczych pomiarów w celu okrc c i wyników res/towych. które prawdopodobnie wykazują te same cechy ro/kbJ.;» związku z tym mogą zostać ze sobą połączone. Reszty te (wyniki res/towei f>vai zbadać pod względem wartości skrajnych, skośności. kurtozy bądź innych od rozkładu.

Obliczenie prostych statystyk opisowych na wynikach res/towych częstop> maga wykryć nienormalność rozkładu. Można na przykład obliczyc wskaźnik skośności i kurtozy rozkładu z próby i porów nać je z wartościami oc/ckiwinyra przy normalności rozkładu. Jeżeli skośno.ść rozkładu z próby nie jest Noka ten

_W. « !»«*<* (»m.«ńw nta KU    „,_y Irt,, ^

"*jUul K»< *<>** ^dnd'^,m" ł~ “rt™- -/U.1 jr -1    V**^-

£>,*.* kurto/* m/kUlo / pn*y    „ „    ’, ~

‘ _ktfrtyc/ny <uK*nny>- ^alh" tep*‘»kurl>c/ay (dndalmi

⁰¹ siuteivn>m npmohcrt. /badanu rń/n>ch cech ro/kb* pnmm*

.M*i> '« n.«i.»ln>n, wykrcwrm kw,mylnym _Ahy    ^

^l.aiiykiwy. o.jpicrw MMtejraKmy mny , _P.,*iu_Km-. _K .* . _|(Ml_ ^ do n*ju»<k'/c| Oraac/amy U) na|mn«,_{W4    f M} _

, Tww* <**»**    «"<* kw^™. . ab ..,c,    ™

. Somuln. wanofe kwmtylow, ........«JchyW wnum, .Upou.l,,,

L*<toOodoWetelwu / ni/.s/cj połyki standardu* rp, n//kład.. ooimaln^,. „' *

(«)

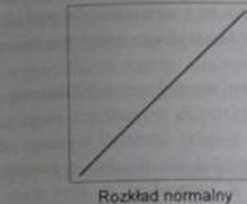
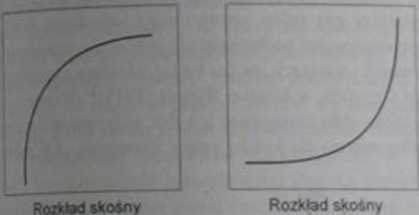
dodatnio

(6)

ujemne

(c)

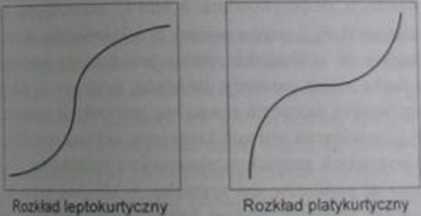
(d)

(•>

k»c |}.|. Normalne wykresy kwantylowc kliku chanktcr>a>t/n«h

ndbdb

285