CCF20140608017

5.3. Wymiar Hausdorffa i wymiar topologiczny 59

Można wykazać [17], [20], że istnieje dokładnie jedna liczba do, dla której

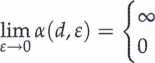
dla d < do dla d > do

(5.9)

Definicja 5.1. Liczbę do nazywamy wymiarem Hausdorffa zbioru F i oznaczamy przez dimH(-f)-

a(d,e) staje się podobne do N_£(F)e^d. Jeżeli teraz dla pewnego ustalonego do istnieje, przy e —> 0, skończona i różna od zera granica lim (N_£(F)e^d°), to do

Istnieje bliski związek między wymiarem fraktalnym i wymiarem Hausdorffa. Gdyby przyjąć, że w pokryciu wszystkie kule mają średnicę e, to

i d(F) = 1.

jest wymiarem fraktalnym zbioru F. Ale granica ta nie zawsze istnieje (albo przyjmuje wartość zero lub nieskończoność), a więc definicja Hausdorffa jest ogólniejsza. Dla wszystkich omawianych dotychczas przykładów fraktali wymiar Hausdorffa i wymiar fraktalny wyrażają się tą samą liczbą, ale ogólnie zachodzi nierówność dimn(F) < d(F). Na przykład dla zbioru F tych punktów odcinka (0,1), które mają wymierne współrzędne, mamy dim^fF) = 0

Poniżej podajemy listę najważniejszych własności wymiaru Hausdorffa.

1.    Jeżeli A C B C Rⁿ, to dim^A) ^ dimH(B).

2.    Jeżeli A = U~₌₁ A„ jest sumą przeliczalnej liczby zbiorów A\ C Ąj C A3 C C ..., to dim^r(A) = sup_n dim.H(A_n). W szczególności każdy przeliczalny zbiór punktów przestrzeni Rⁿ ma wymiar dim^ równy zero.

3.    Jeżeli A C Rⁿ i B C R^m, to dla iloczynu kartezjańskiego A x B C R^n+m zachodzi nierówność dinif/(A) + dim^fB) ^ dim^(A x B).

4.    Dla sumy zbiorów mamy dim^A U B) = max{dimH(A), dimn(B)}.

5.    Jeżeli A jest zbiorem otwartym lub, ogólniej, zbiorem mającym dodatnią miarę Lebesgue'a w Rⁿ, to dim/-/(A) = n.

6.    Jeżeli / jest dyfeomorfizmem, to znaczy wzajemnie jednoznacznym i w obie strony różniczkowalnym (f i /^_1 mają ciągłe pochodne) przekształceniem zbioru A C Rⁿ w zbiór /(A) C Rⁿ, to dim#(/(A)) = = dim_H(A).

Dla podzbiorów przestrzeni Rⁿ mających zerową miarę Lebesgue'a wymiar Hausdorffa może przybierać wszystkie wartości z przedziału od zera do n włącznie.

Obliczanie wymiaru Hausdorffa dla atraktora układu IFS nie jest łatwe, ale dla pewnej klasy atraktorów można skorzystać z następującego twierdzenia

[17].

Twierdzenie 5.1. Niech Aoo będzie atraktorem układu iterowanych odwzorowań [R²; W\,W2,. ■ -/Wk}, w którym odwzorowania zwężające są podobieństwami

(5.10)

Wi{z) = ajZ + C{ albo W{(z) = a_;z* + c_;-