1629289608

1. Wiadomości wstępne

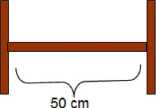
Rysunek 1.2.

Zadania

Ćwiczenie 1.1. Ile półek o wymiarach 30 x 50 można wykonać z 9 desek długości 130 cm.? Rozwiąż zadanie graficznie.

Ćwiczenie 1.2. Przy warunkach zadania 1.1 wylicz ile desek potrzeba na wykonanie 11 pólek. 1.2. Zbiory wypukłe i zbiory domknięte

Zagadnienie optymalizacji polega na znalezieniu minimum lub maksimum funkcji f : X —> R, gdzie X jest podzbiorem R” zwanym obszarem dopuszczalnym. Od zbioru X wymagamy by był domknięty i wypukły.

Zaczniemy od opisania najważniejszych własności zbiorów wypukłych i domkniętych.

Definicja 1.1. Podzbiór A C Rⁿ nazywamy domkniętym jeżeli granica każdego zbieżnego ciągu punktów z A należy do zbioru A. Lub równoważnie: Jeżeli punkt p nie należy do A to istnieje e > 0 taki, że kula o środku p i promieniu e jest rozłączna z A. Symbolami zapisujemy to: P&A => 3_e>o %e)nJ = 0.

Będziemy też używać znanego twierdzenia o zbiorach domkniętych.

Twierdzenie 1.1. Część wspólna zbiorów domkniętych jest zbiorem domkniętym.

Definicja 1.2. Domknięciem zbioru A C Rⁿ nazywamy zbiór A — fili? | A C B A B domknięty} czyli najmniejszy zbiór domknięty zawierający A.

Jedną z najważniejszych własności obszaru dopuszczalnego jest wypukłość.

Definicja 1.3. Wypukłość

Podzbiór A C Rⁿ jest wypukły jeśli wraz z każdymi dwoma punktami zawiera odcinek łączący je, czyli:

V_p,_geA pqC A