Dziawgo; Macierz odwrotna Równania macierzowe 1

66 Wyznacznik i rząd macierzy

66 Wyznacznik i rząd macierzy

1	4 1	2				1	2	3	0
2	1 -1	1			d)	2	4	1	1
3	2 2	4				3	2	3	1
4	3 3	2				1	1	2	1
						2	2		2	-1	-2	1
2	2	2	-1	-2		-1	1		1	2	1	5
-1	1	1	2	1		1	3		1	-2	-1	0
1	3	1	-2	-1	f)	2	-1		5	3	-1	3
2	-1	5	3	-1		-1	-2		-1	1	1	-1
-1	-2	-1	1	1		1	0		1	2	-1	2

7.4 Rozwiązać równania wyznacznikowe:

c)

^e)

a)

c)

1 4	-3	-1				0	1	X	-3
x -3	4	1		-2x + 4,	b)	X	1	4	-3	_
0 -3	X	1				1	-1	-3	4
1 1	-1	0				1	0	-1	1
2 0	1		-1			0	-1	X		3
1 -1	-2		1			-1	2	1	2
				= 17,	d)
x^2 3	-1		X			1	0	-1		2
-1 2	1		0			-2	3	2	1

= -4x + 9,

= 6x² -12.

7.5 Obliczyć rząd macierzy:

"1	1	-1	2"
					”-3	1	1	-l"		"1	1	-4	0	3 “
1	2	-2	3		-2	2	1	1	,c)	1	-1	-2	-2	-2
0	2	1	1	,b)	1	1	1	3		1	-3	0	-4	0
0	5	-2	6		_-3	1	2	1 _		0	1	-1	1	1
1	3	0	3_

a)

7.6 Dla jakiej wartości parametru a rząd macierzy jest równy 3.

				a	1	0 -f
	“ -2 -1	a 0"	b)	1	0	-1 -a
a)	2 a - 1 3	-a-2 1		-1	a	2 1
	a-l 2	a 1		a	-a	1 a

Ćwiczenia 8

Macierz odwrotna. Równania macierzowe

Zadanie 1.

M.ilr/ć macierz odwrotną do macierzy A=

2	-1	1
3	2	2
1	-2	1

Rozwiązanie:

• i l lasyczna metoda wyznaczania macierzy odwrotnej.

dcl A = det

2	-1	1
3	2	2
1	-2	1

Macierz odwrotną znajdziemy korzystając ze wzoru

A"¹ =■

= 5

detA

gdzie dy jest dopełnieniem algebraicznym elementu ajj macierzy A.

	2	2			3 2
,, ( I)^2	-2 1		= 6	d,,=(-i)^3	1 1	= -l	di3=(-l)^4
	-1	1			2 1
( 1)'	-2	1	= -l	d22^=(" l)^4	1 1	= 1	d23=(-l)^5
	-1	1			2 1
u ( D'^1			= -4	d32=(-l)^5		= -l	d33=(-l)^f'
	2	2			3 2
		6	-1 -8		6	-1 -4"
1)		1	1 3	, D^1	1	1 -1
		4	1 7		K	1 7

-1

2

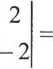
-8

-1

-2

= 3

= 7

1

•• l|*«twiednie elementy dopełnień algebraicznych elementów macierzy A wyno-