Dziawgo; Macierz odwrotna Równania macierzowe 3

70 Macierz odwrotna. Równania macierzowe

Zadanie 3.

Wykorzystując macierz odwrotną, rozwiązać względem X równanie macierzowe:

1 3 4 2

X =

3    2

4    6 '

Rozwiązanie:

Równanie to można zapisać w postaci AX=B. Jeżeli macierz A jest nieosobli wa, to istnieje do niej macierz odwrotna A'¹. Jeżeli pomnożymy lewostronnie obie strony równania przez macierz A^-1 to otrzymamy :

A^aAX=A'¹B, czyli I X = A''B i X=A''B

det A = -10

A'¹ =

-0,2

0,4

0,3

-0,1

"-0,2 0,3 “	“3 2		“0,6 1,4"
_ 0,4 -0,1	_4 6_		0,8 0,2_

Zadanie 4.

Rozwiązać względem X równanie:

3 4 5 6

X-

1 2

3 2

-3 4

2 1

Rozwiązanie:

Jest to równanie postaci AXB=C. A"¹AXBB'¹=A"¹CB'¹ 1X1 =A"¹CB'¹ X=A~¹CB‘¹

Macierze A, B są nieosobliwe, istnieją wię< macierze odwrotne A'¹, B'¹.

Mnożymy obie strony równania lewostronni. przez A'¹ i prawostronnie przez B'¹.

* i 1	" 6	-4"	, 1	“ 2	-2“
detA= -2 , detB= -4 A =-- 2	-5	3	’ ^B t4	-3	1

1	6 -4"	'-3 4"	2 -2“	_ 1	-112 9"
8	-5 3_	_ 2 1_	-3 1_	~ 8	93 -59

/ silanie 5.

	2	1 2		4	5	6
N że A=	1	2 2	,B=	2	3	1
	1	1 2		1	1	1
		ET^1-	(x-‘	+ l)	f	-1

= A • B.

rozwiązać równanie macierzowe:

Rozwiązanie:

li ^1	(X-^1	^+ I) J		—	= A^-1 -B
		T~1	- i
(^x	^+ Iy	_	F		') = A“ B
	i	t"1	-1
(^x	^+ lJ			B	II > 1 OT

-1

(X '+|)

= A^-1 BB^_I

Wykorzystując własności odwracania i transponowania macierzy doprowadzamy równanie do prostszej postaci.

Wykorzystujemy własność

(MN)'oraz

Mnożymy obie strony równania prawostronnie przez B‘ (13 jest nieoso-bliwa).

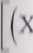
T

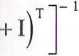
•I = A"

•I

Ponieważ M * M'^I=I.

(X

-i- A

- i

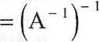
Odwracamy macierze po obu stronach równania.

Wykorzystujemy własność

(M'¹)^t=(M^t)'¹ , (M-N)^t=M^t-N^t, (M^t)^t=M.

( X ¹ fl)^T = A

(X ^,)'+I^t=A ( X ')' = A-T^t

!(x ¹)¹ )^T = (a — I^T)‘

Wykorzystujemy własność

(m + n)^t = M^t + N^t.

Przy założeniu, że istnieje macierz odwrotna do macierzy (A¹-!).

\ ¹ A^r-I (X ') ' (a¹ i)

X (A¹' l) '