Dziawgo; Macierz odwrotna Równania macierzowe 4

72 Macierz odwrotna. Równania macierzowe

72 Macierz odwrotna. Równania macierzowe

2	1	2	T	"l	0	o"		~2	1	f		"l	0	o"
1	2	2	-	0	1	0	=	1	2	1	-	0	1	0
1	1	2_		0	0	1		2	2	2		0	0	1_

1

1

1

1 1 1 1

2 2

Ponieważ wyznacznik macierzy A¹-! jest równy zero, zatem nie można wyzna czyć macierzy odwrotnej. Dane równanie dla zadanych macierzy nie ma roz wiązania.

Zadanie 6.

Rozwiązać równanie macierzowe:

/ T \1~ 1	i to >— o o 1		“0 f
X • ^A ^r • AJ = B, gdzie A =	-1 2	, B =	_2 1_
	-1 1

Rozwiązanie:

Wykorzystując podstawowe własno,I na macierzach przekształcamy dom równanie macierzowe doprowadzaj<i> je do prostszej postaci.

X-(a^t-A) = B“‘

A^tA jest macierzą kwadratową, j< \f ,    .    ,    _ i odwracalna o ile wektory macierr \

X • (A • AJ • (A • AJ — B • ^A • Aj _n\_{e S}ą wspólliniowe.

x = (a^t-a-b)“'

A^t • A-B =

1 2 0 0

	" 1 2"
	2 0		"0 f
	-1 2		_2 1_
	-1 1

-1

2

" 7	-f	^_0	f		"-2	6“
-3	5	2	1		10	2

W \ nncznik macierzy A¹ • A • B wynosi -64. Zatem można daną macierz od-»v h». ii-. Wykorzystując klasyczną metodę odwracania macierzy otrzymujemy:

X = -

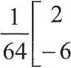
-10

-2

/ v I) A NI A

	“1	2	3~		'0	1	3“
» i 1 >la macierzy A =	4	5	6	, B =	2	0	1
	1	0	2		3	4	2

sprawdzić następujące

lasności macierzy odwrotnej: a) (AB)’¹ = B'¹ A'¹,    b)(A'^]y'=A,

c)(kB)-‘= j-B-¹, k

• I) dot A =■

1

det A

e) A'‘B=BA'^,C>AB“ =B"A

¹¹ l klórej z niżej podanych macierzy istnieje macierz odwrotna:

1 2 3^_
		4 0		^_1 2 3"
4 5 6	, B =		, C =
		5 0		4 2 5
0 1 2

" i olnii.

• ^ Hu \Mi|/ać równania macierzowe:

.») (A ⁱ.X^t-A)“'+[a^t-B-(A“^,)^t]^T=I, gdzie

1 2

3 4

A

'1 2'

1 2

H ' W , i lac/.yć macierz odwrotną do macierzy A=

" ^{1 1} 'la jakich wartości a istnieje dla macierzy A=

5 2 1 3 4 2 0 2 0

3 4 a 1 2 1 -12 0

macierz od-