Macierz odwrotne, równania macierzowe (22)

md. 2 Za pomocą macierzy odwrotnej rozwiąż równanie macierzowe:

a)    AK + BX = X + A gdzie

	' 1	0	1'		2	-1	1 ’
A =	2	1	1	B =	-1	0	0
	. 0	0	3 .		. -2	1	0 .

b) AX = BX — 21    gdzie

d) A — X • A — I

gdzie A =

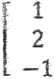
0

-1

2

3

0

1

	• 3	1	-1 '		’ 1	2	-3 •
A =	-2	2	2	B =	-3	2	1
	. -1	2	3 .		. 1	1	1 .
AX-		B =	A	gdzie
	‘ 1	3	5 '		’ -3	0	0
A =	-1	0	-2	B =	0	-3	0
	. 1	1	1 .		. 0	0	-3

$)    XA - B * A    ndzie

	' 1	3	5 ‘			-3	0	0
A =	-1	0	-2	B =		0	-3	0
	. 1	1	1 .			0	0	-3
XA =	XB-	21		gdzie
	^r 3	1	-1 1			1	2	-3
A =	-2	2	2	S =		-3	2	1
	. -1	2	3 .			1	1	1 .

g) XA + XB = X + A gdzie

	’ 1	0	1 ■		2	-1	1 '
	2	1	1	}. —	-1	0	0
	. 0	0	3 .		. -2	1	0 .