Funkcje trygonometryczne1

26

FUNKCJE TRYGONOMETRYCZNE

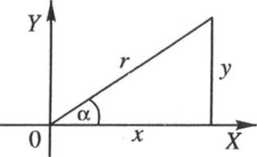
Definicje

y

sin a = -

X

cos o. — — tga = 7 (**0) ctg a = “ (y*0)

/ ^y

r ⁹    r

sec a = - (jr*0) cosec a = - (y*0)

■*    y

Wzory podstawowe

tga = -

sin² a + cos² a = 1 cos a

ctga =

sin a

tg a =

ctga

Wartości funkcji trygonometrycznych wybranych kątów

a		sin a	cos a	tg a	ctga
radiany	stopnie
0	0	0	i	0	—
71 Tl	15	V6-<2 4	<6+Ś2 4	2-VT	2 + VF
n JO	18	Ś5-1 4	V 10 + 2^5 4	V 25 - ltWif 5	'15 + 2'ts
n S	22- 2	■fen 2	V2 + V2 2	V2-l	V2 + 1
TC 5	30	1 2	V3 2	V3 3	V3
TC ?	45	V2 2	<2 2	1	1
TC I	60	V3 2	1 2	V3	V3 3
5 72*	75	Vó+y/2 4	<6-<2 4	2 + V3	2-vr
TC *	90	1	0	—	0
TC	180	0	-1	0	—
3 2*	270	-1	0	—	0
2 TC	360	0	1	0	—

Wzory redukcyjne

<p		sin <p	cos (p	tgtp	ctg tp
-a	-a	- sin a	cos a	-tg a	-ctga
90° +a	n/2 + a	cos a	- sin a	-ctga	- tg a
90°-a	tt/2-a	cos a	sin a	ctg a	tga
180° +a	Ti + a	- sin a	- cos a	tg a	ctg a
0 1 c oc	Ti -a	sin a	-cos a	-tg a	-ctga
270° + a	lótt + a	- cos a	sin a	- ctg a	- tg a
270°-a	’/ó7t + a	- cos a	- sin a	ctg a	tg a
360° +a	2tt + a	sin a	cos a	tg a	ctga
360° -a	2tt-a	- sin a	cos a	- tg a	- clg ot

Przykład: cos (180° + a) = -cos a

Funkcje kąta podwojonego

2 ig a

l+tg^{1 2}a

sin 2a = 2 sin a cos a =

cos 2a = cos² a - sin² a = 2cos²a -1 = 1-2 sin²a = -———

tg 2a =

2 tg a

ctg 2a =

I + tg- a ctg² n - I ctg a - tg a

I - tg a ctg a - tg a    2 ctg a    2

Uwaga! W tych oraz następnych wzorach zakłada się, żc wszystkie użyte wyrażenia są określone. Funkcje kąta połówkowego

sin^	— + A	/ 1 - cos a	cos“ = ±-\^	^1 1 + COS ('
	* \	/ 2		2
<■!		/ 1 - cos a	sin a 1 - cos a
	* \	1 1+ cos a	1 + cos a sin a
. ^actg y	- + A	1 1+ cos a	1 + cos a sin a
	^1 >	V 1 - cos a	sin a 1 - cos a

Uwaga! Znak + lub - we wzorach zależy od tego. do której ćwiartki układu współrzędnych należy —.

Funkcje sumy i różnicy kątów

sin (a+(5) = sin a cos p + cos a sin p cos (a+P) = cos n cos p - sin a sin p sin (a-P) = sin a cos p - cos a sin P cos (a-P) = cos et cos p + sin a sin P

tg (a+p) = -ctg (a+P) =

tg (a-P) = ctg (a-P) =

tg a + tg P I - tg a tg p ctg a ctg p - I ctg p + ctg a

tg a - tg P

1

+ tg a tg p

2

ctg a ctg P + I ctg p - ctg a