Image42

82
82
ku górze przedstawiono na
Przypadek stożka zwróconego wierzchołkiei rys.24. Mamy więc
u _ H
x ” R’
V(y)

2 du
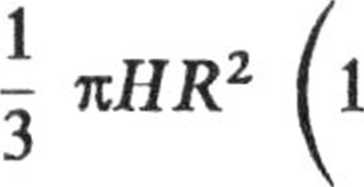
H
Wtedy

W = ^ ngpHRz 1
H
dy
\ ngpR2H2 4
2.19. Praca zostaje zużyta na pokonanie siły ciężkości działającej na piramidę, podnoszącą się z powierzchni ziemi (rys.25). Zmieniającą się objętość piramidy
obliczamy ze wzoru
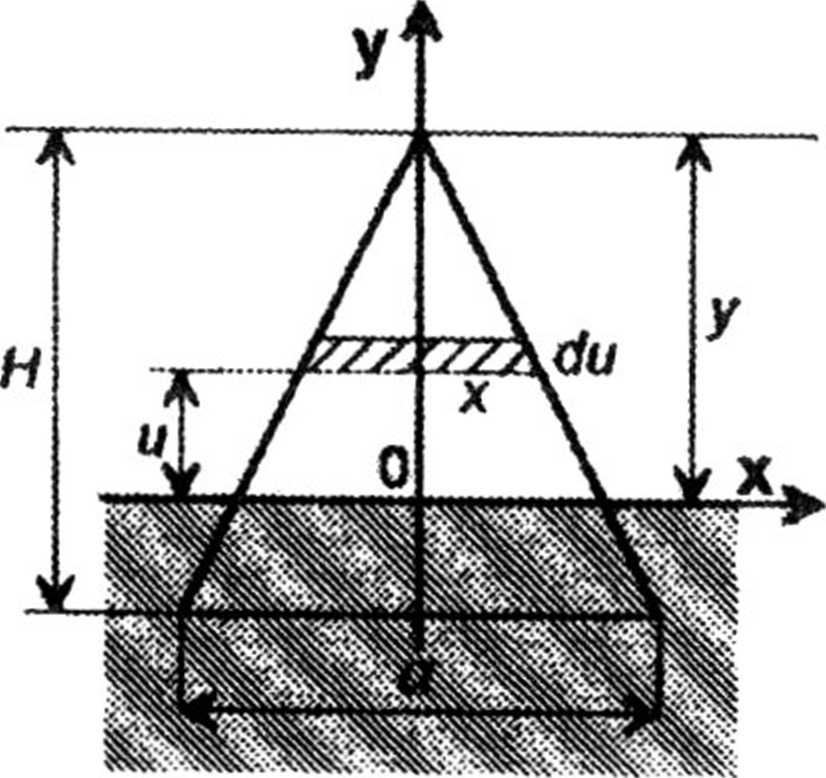
Rys.25
V(y)
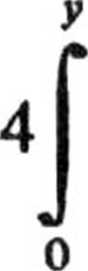
x2 du =
2 3
aAy
3 H
2 »
gdzie x znaleziono z proporcji
y - u
H
a
2
Stąd szukana praca
W = FJy) dy

y a

y3 dy=
1
2tj2
Podstawiając dane liczbowe mamy
W « 1,63 * 1012 [Nm].
2.20. Aby usypać stos piasku w kształcie stożka, należy wykonać pracę
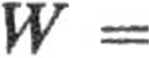
1
12
nyR2H2.
II
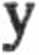
Wstawiając do tego wzoru dane liczbowe ma
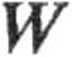
11 775 [Nm].
2.21. Praca włożona jest równa
gdzie yw jest ciężarem właściwym wody.
2.22
I sposób. Praca siły F przy przemieszczeniu punktu od P1 (x, y) do P2 (x, y) wyraża się całką krzywoliniową po drodze l (rys.26)
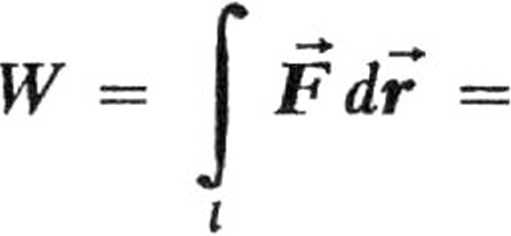

Fx dx 4- Fy dy

— e* cosy dx 4- ex
siny dy.
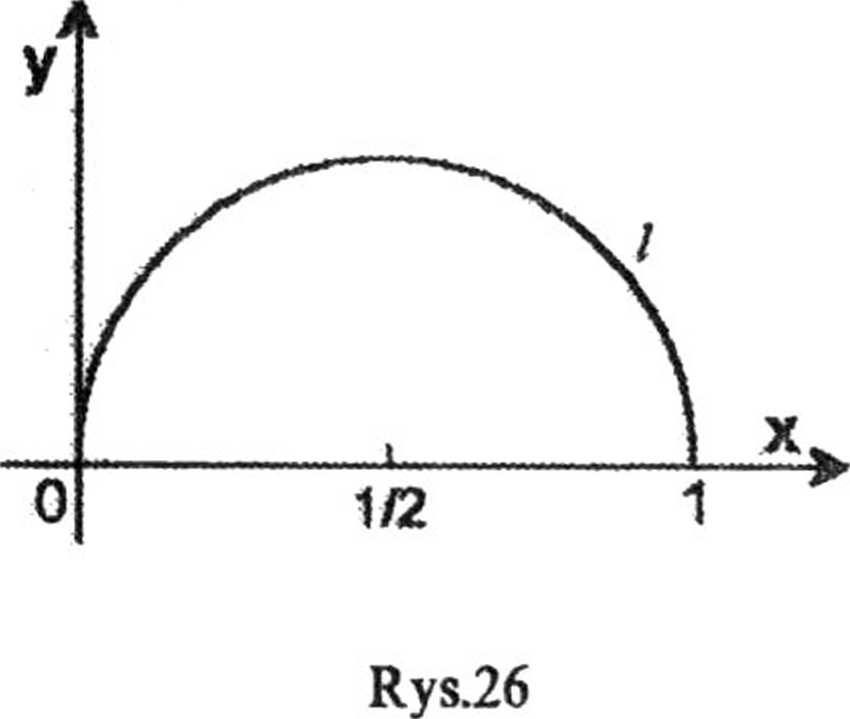
Krzywoliniową całkę skierowaną zamieniamy na całkę oznaczoną, wprowadzając parametryzację krzywej /:
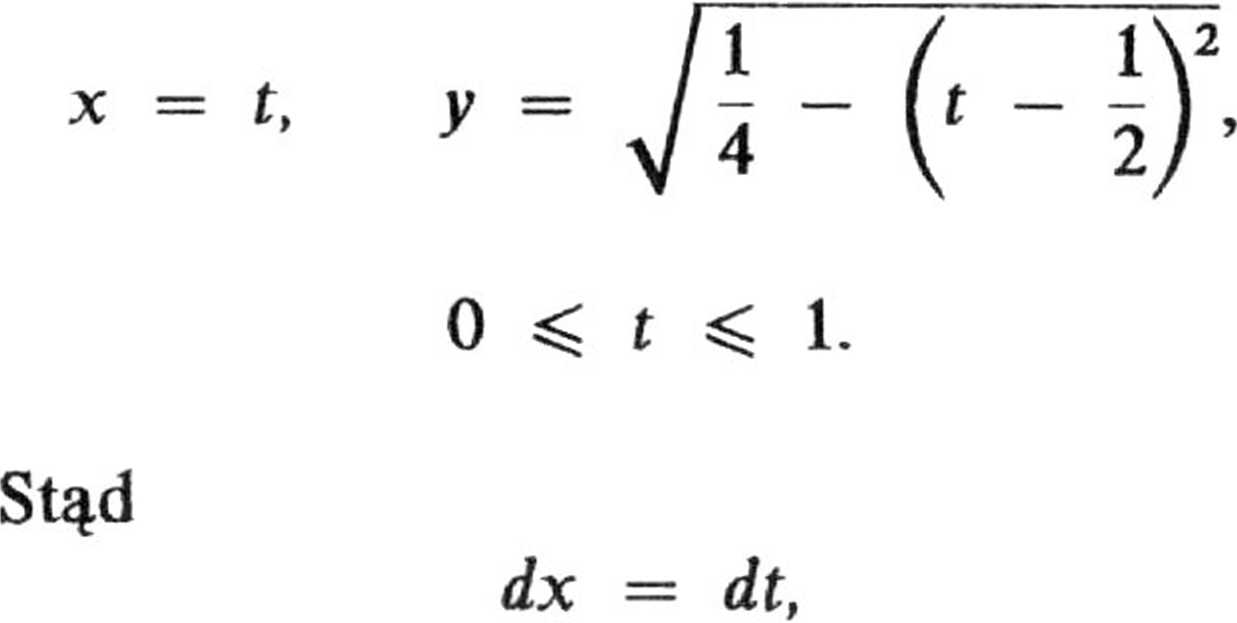
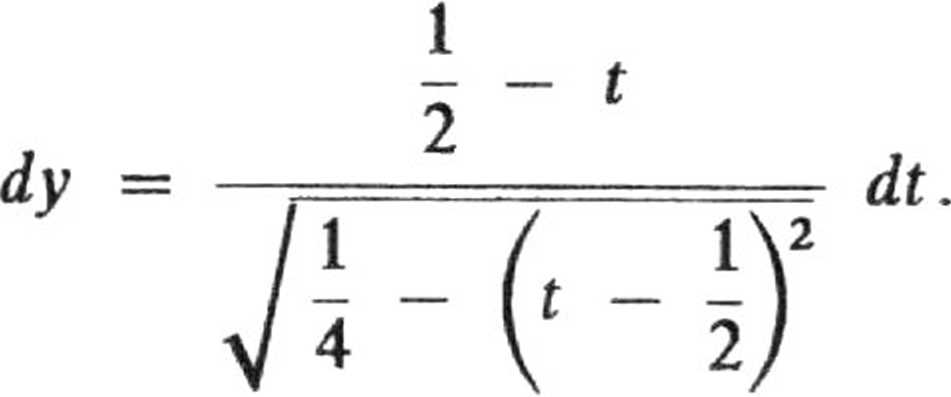
Wyszukiwarka
Podobne podstrony:
31070 Image42 (16) 82 82 ku górze przedstawiono na Przypadek stożka zwróconego wierzchołkiei rys.24.
Image463 Wykorzystując schemat ideowy układu przedstawionego na rys. 4.566 i schemat ideowy układu p
str002 , Które 2 poniższych stwierdzeń jest/są poprawne -Trzon mostka ku górze sięga na wysokość dru
SCAN0165 9 tif ku całego przedsiębiorstwa na skuteczność działań oddziału. Ogólnie jednak formułę PR
18781 str002 , Które 2 poniższych stwierdzeń jest/są poprawne -Trzon mostka ku górze sięga na wysoko
image 59 (3) aby łezka B była skierowana ku górze, a łezka A - na dół. Zaczynamy wyrabiać łuczek z p
image40 2 Rodzina państwa Duchowskich także była na wycieczce. Właśnie z niej wrócili. Wszyscy sq gł
wyczesany słownik�6 niem, jakie ciśnie mi się teraz na usta jest »totalna schiza«”. jednej strony, m
CCF20081202�009 Posiewając badany materiał na powierzchnię pożywki uprzet nalanej (rys. 24) i zestal
Image492 się przełącznikami Ku K29 Kz, KA. Działanie układu jest zbliżone do działania układu, przed
więcej podobnych podstron