31070 Image42 (16)

82
82
ku górze przedstawiono na
Przypadek stożka zwróconego wierzchołkiei rys.24. Mamy więc
u _ H
x ~ R’
V(y)

2 du

y
H
Wtedy
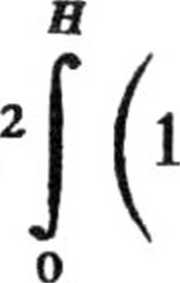
H
dy =
! ngPR2H2 4
2.19. Praca zostaje zużyta na pokonanie siły ciężkości działającej na piramidę, podnoszącą się z powierzchni ziemi (rys.25). Zmieniającą się objętość piramidy
obliczamy ze wzoru
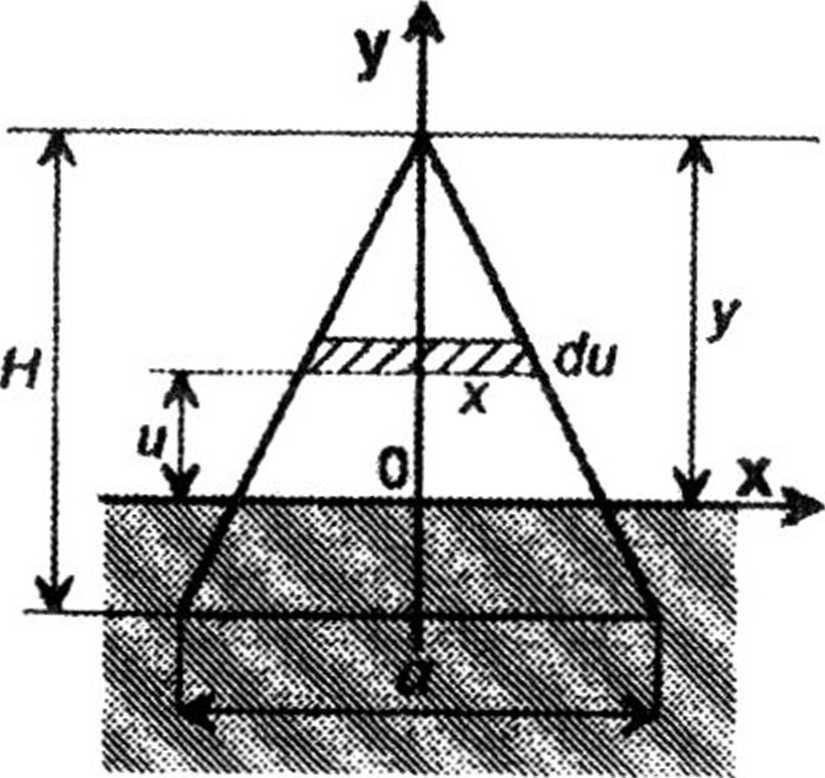
Rys.25
V{y) =
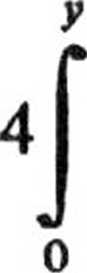
x2 du
a2y3
3 H
2 »
gdzie x znaleziono z proporcji
y - u
H
a
2
Stąd szukana praca
W = F Jy) dy

ya

y3 dy =
i
2 rj2
12
yazH
Podstawiając dane liczbowe mamy
W » 1,63 ♦ 1012 [Nm].
2.20. Aby usypać stos piasku w kształcie stożka, należy wykonać pracę
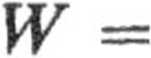
1
12
TvyR2H2.
II
Wstawiając do tego wzoru dane liczbowe ma
rs-/
11 775 [Nm]
2.21. Praca włożona jest równa
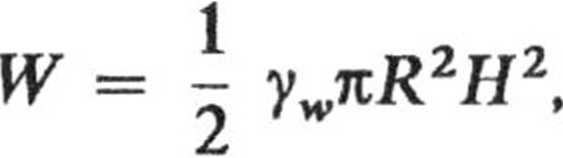
gdzie yw jest ciężarem właściwym wody.
2.22
I sposób. Praca siły F przy przemieszczeniu punktu od P1 (x, y) do P2 (*, y) wyraża się całką krzywoliniową po drodze l (rys.26)
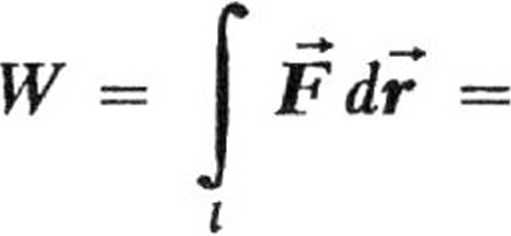

Fx dx 4- Fy dy

— e? cosy dx 4- e*
siny dy.
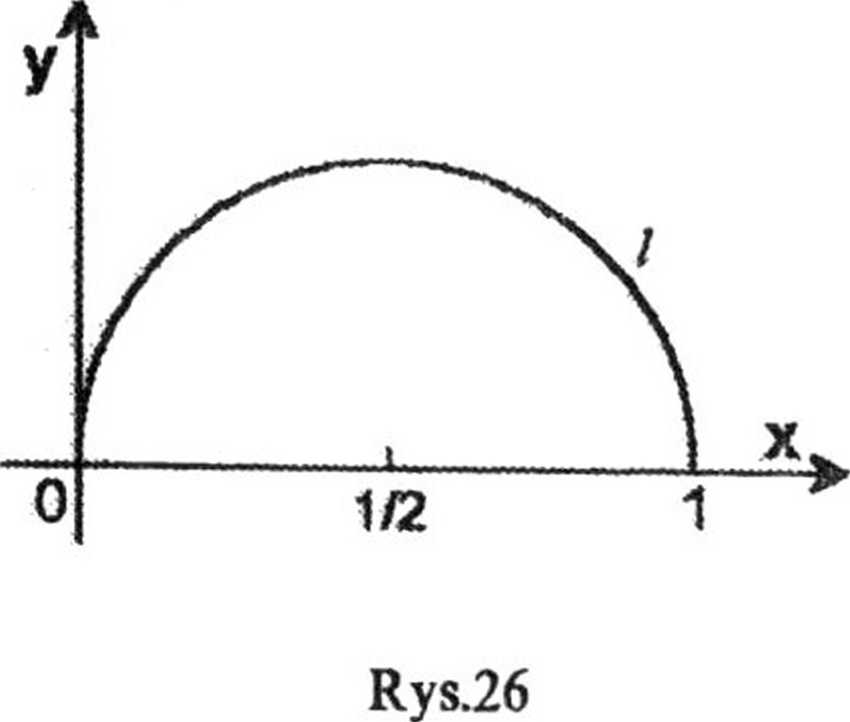
Krzywoliniową całkę skierowaną zamieniamy na całkę oznaczoną, wprowadzając parametryzację krzywej /:
|
X — t, |
' = , |
- 9 • | |
|
• V/ V/ o | |||
|
Stąd |
dx = |
= dt, | |
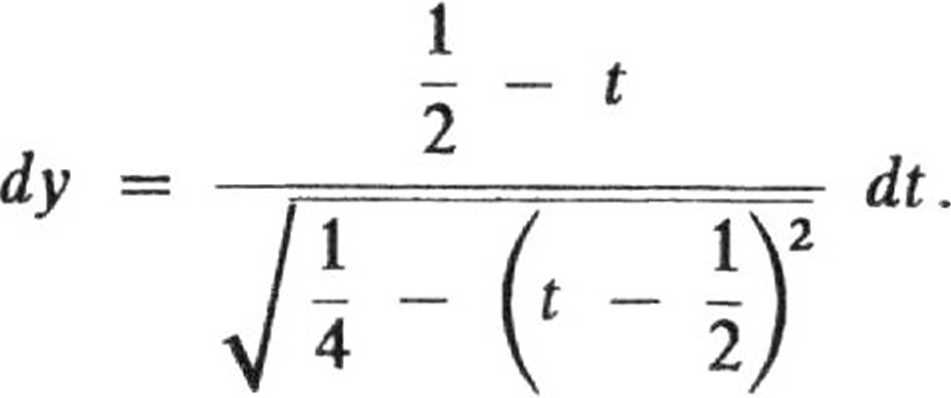
Wyszukiwarka
Podobne podstrony:
Image42 82 82 ku górze przedstawiono na Przypadek stożka zwróconego wierzchołkiei rys.24. Mamy więc
str002 , Które 2 poniższych stwierdzeń jest/są poprawne -Trzon mostka ku górze sięga na wysokość dru
SCAN0165 9 tif ku całego przedsiębiorstwa na skuteczność działań oddziału. Ogólnie jednak formułę PR
18781 str002 , Które 2 poniższych stwierdzeń jest/są poprawne -Trzon mostka ku górze sięga na wysoko
image 59 (3) aby łezka B była skierowana ku górze, a łezka A - na dół. Zaczynamy wyrabiać łuczek z p
lichtarski (8) 16 1. Przedmiot i ewolucja nauki o prwltiębiorłtww przedsiębiorstwa i na zewnątrz, do
Image492 się przełącznikami Ku K29 Kz, KA. Działanie układu jest zbliżone do działania układu, przed
więcej podobnych podstron