img074

Przykład 5-9. Określić momenty bezwładności względem osi środkowych główny^ przekroju jak w przykładzie 5-3 (por. rys. 5-6). Odczytane z tabl. 14-26 momenty bezwładnoś_Cj ceownika 240 względem osi przechodzących przez jego środek ciężkości oraz pole przekroj_u ceownika wynoszą: 7_A| - 3600 cm⁴, I_y = 248 cm⁴, A = 42,3 cm².

Momenty bezwładności obliczono od razu względem osi środkowych głównych x₀, y₀ (p_0f rys. 5-6). Otrzymano:

30 • 2³

I_Xq =    ^    +30-2(1 + 12 — 5,39)² + 2 • 3600 + 2 • 42,3 • 5,39² = 13 153 cm⁴,

2-30³

7_V =-+ 2 • 248 + 2 • 42,3(4 + 2,23)² = 8279 cm⁴.

^yo 12

Przykład 5-10. Określić momenty bezwładności względem osi środkowych głównych przekroju przedstawionego na rys. 5-13.

Przekrój ma dwie osie symetrii, które przecinają się w jego środku ciężkości C. Osie te są osiami środkowymi głównymi. Z tablicy 14-24 odczytano następujące dane, charakteryzujące dwuteownik 240:

A_x = 46,1 cm², I_Xi = 4250 cm⁴, I_yi = 221 cm⁴. Momenty bezwładności względem osi środkowych głównych:

I_x =27 = 2 • 4250 = 8500 cm⁴,

*0 g    *1

I_v =2/_v + 2A.a² = 2-221 + 2• 46,1 -9² = 7910 cm⁴.

>0s    >1

5.3. Wskaźniki wytrzymałości na zginanie i promienie bezwładności przekrojów

Wskaźniki wytrzymałości przekroju na zginanie [cm³, m³] oblicza się jako ilorazy momentów bezwładności przekroju względem osi środkowych głównych i odległości skrajnych włókien przekroju od tych osi. Na przykład w wypadku przekroju symetrycznego względem osi y (rys. 5-14) jest:

W* =

wi =

*09

W_y =

^y0g

(5-l5a)

(5-l5b)

Promienie bezwładności przekroju [cm, m] oblicza się jako pierwiastek kwadrato" > ilorazu momentu bezwładności względem osi i pola powierzchni przekroju:

h

a=90

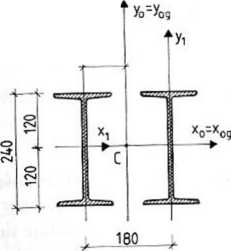
Rys. 5-13 Wymiary w (mm)

y=y₀,

c r 1 ^Amax	f*mox

*

Xog

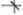
Rys. 5-14

(5-16)

Jeżeli uwzględni się momenty bezwładności względem osi głównych środkowych, to otrzyma się główne środkowe promienie bezwładności przekroju.

Wskaźniki wytrzymałości przekrojów na zginanie oraz promienie bezwładności wybranych przekrojów i kształtowników można określać wg danych tabl. 14-6 oraz 14-24^14-29.

Przykład 5-11. Obliczyć wskaźniki wytrzymałości na zginanie przekrojów rozpatrywanych w przykładach 5-7, 5-8 i 5-10.

Po uwzględnieniu odpowiednich danych otrzymuje się: a) przekrój wg rys. 5-11 (przykład 5-7):

Ix_n. 389900

y*	29,9
ix Og	389900
yj	30,1
r.	35157
Xnwx	15
kład 5-8)
L *0g	121677
y»	15,6
ix ^xOg	121677
yi	24,4
**Og	61771
t Y ^max	20

3885 cm³,